《Attention Is All You Need》 笔记
Posted on 2025-10-11 23:30 in Algorithm
Note
背景知识:encoder-decoder
encoder-decoder 模型是 NLP 领域的概念,不是指具体的算法,而是一类算法的统称,是一个通用框架,在这个框架下可以使用不同算法解决不同任务。
encoder 的作用:将现实问题转化为数学问题。
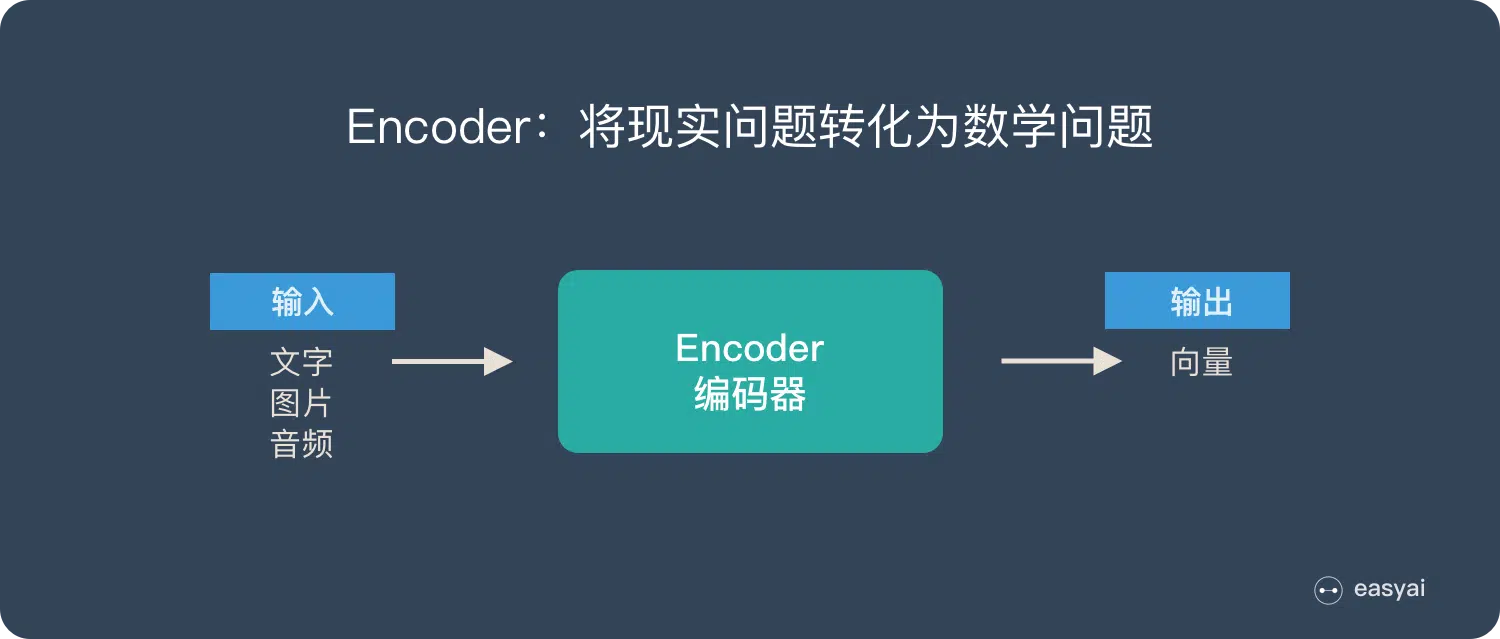
decoder 的作用:将数学问题转化为现实问题。
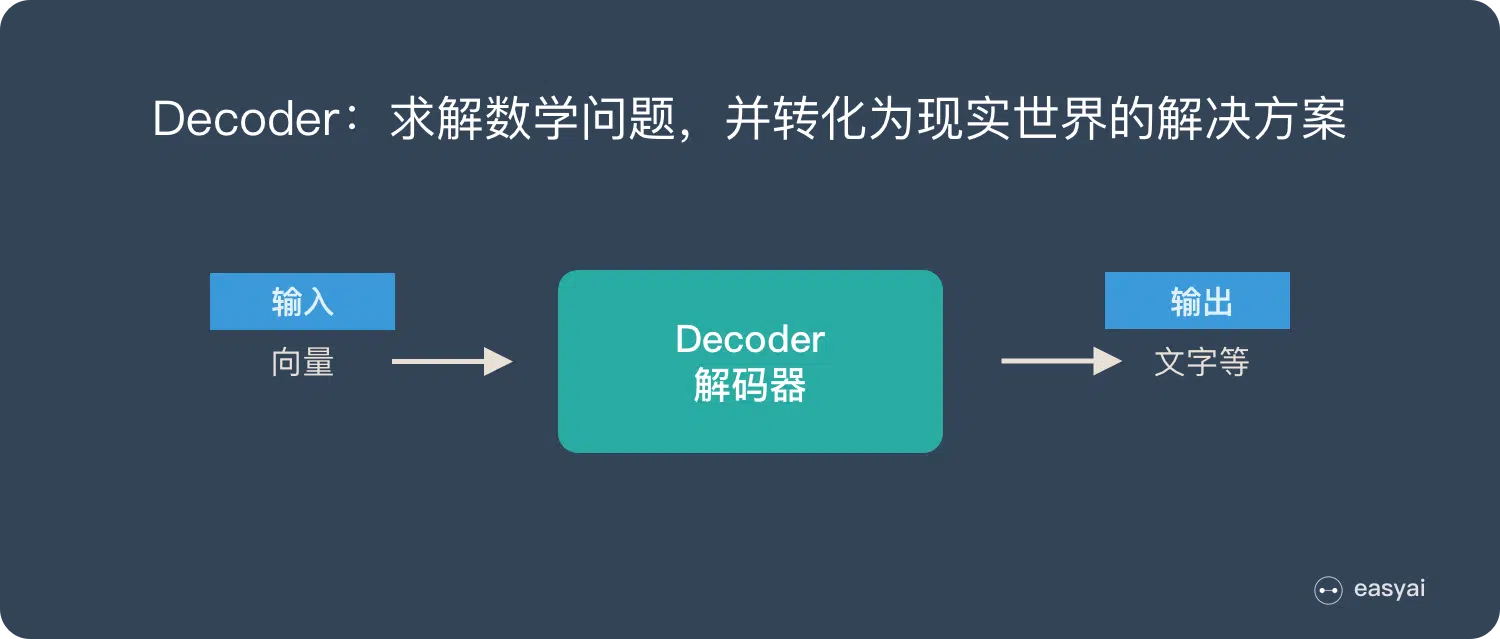
两个连在一起:
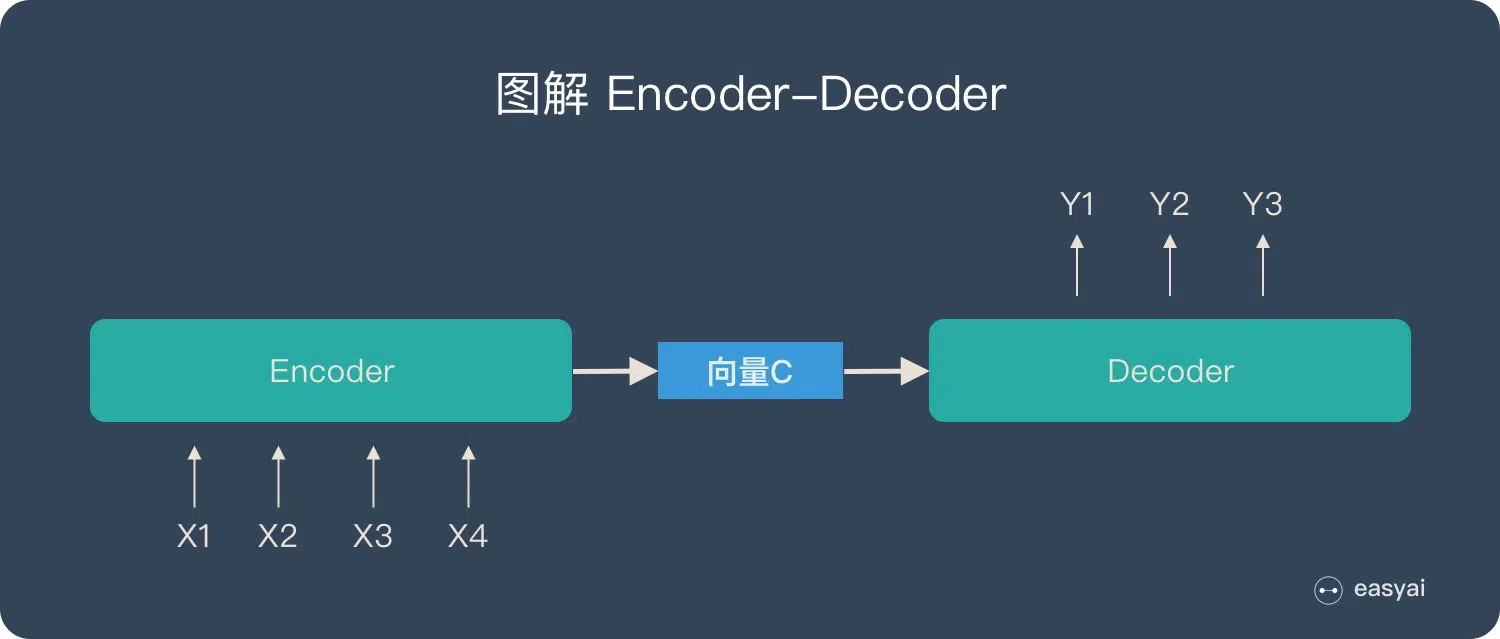
需要注意的两点:
- 无论输入输出的长度是多少,中间向量 C 的长度固定,显然长序列会有数据损失。
- 根据任务不同,encoder 和 decoder 可以用不同的视线,如 RNN,LSTM 或 GRU 等。
Note
背景知识:seq2seq
seq2seq 如字面意思,输入一个 sequence,输出一个 sequence,重点在于 sequence 的长度是可变的。
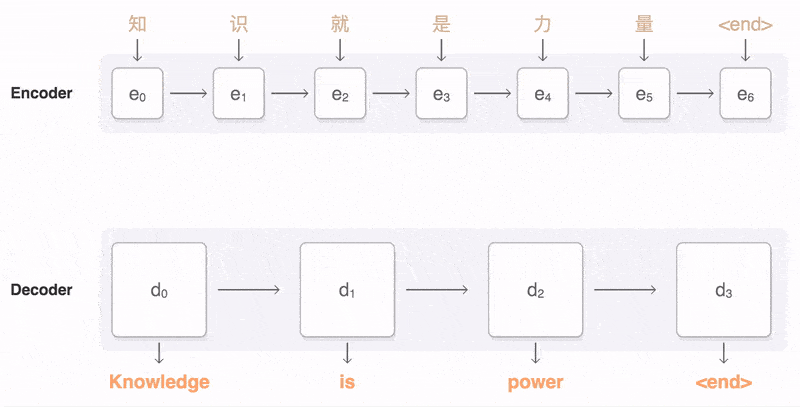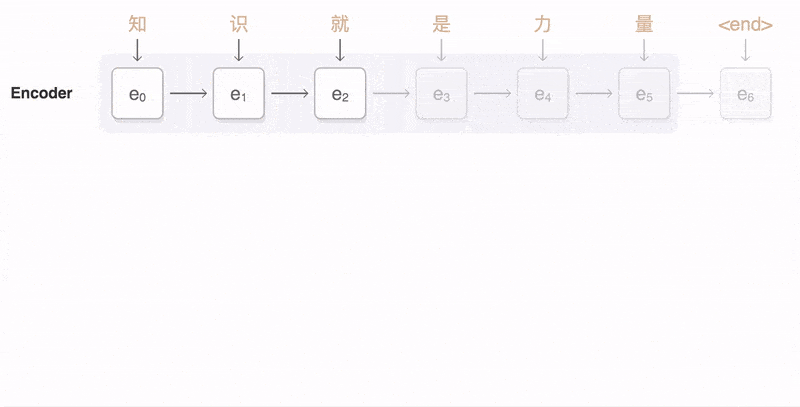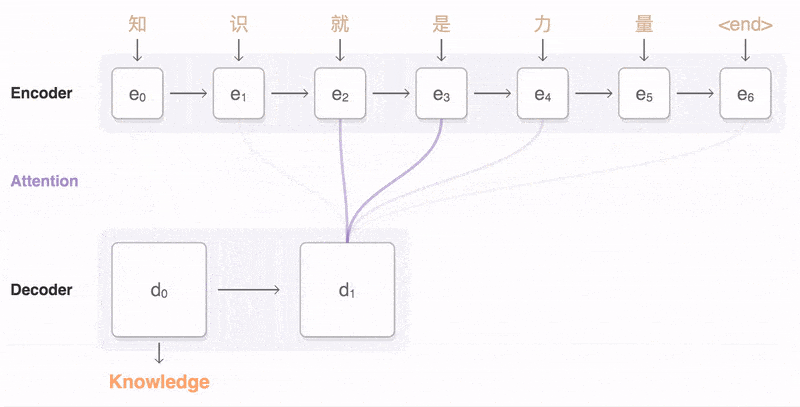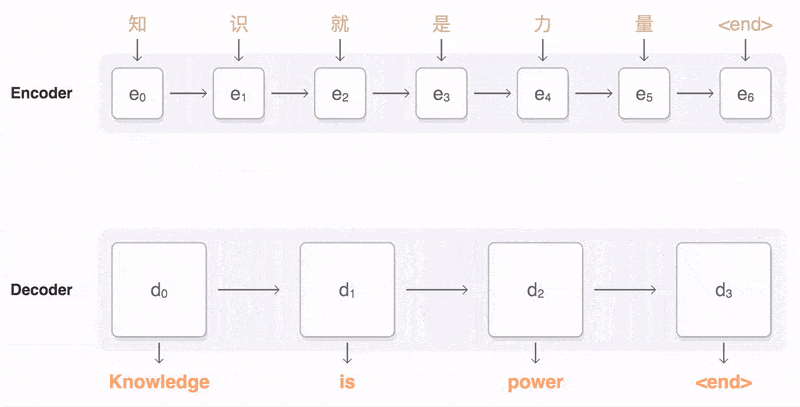
典型的序列转换模型通常包括一个编码器(encoder)和一个解码器(decoder)。encoder 负责将输入序列编码成一个固定长度的隐状态表示,而 decoder 则利用这个隐状态表示生成目标序列。
在这些模型中,循环神经网络(RNN)和卷积神经网络(CNN)是从前最常见的架构。然而,2017 年以来,基于注意力机制的 Transformer 架构(即本论文介绍的架构)因其并行计算能力和处理长距离依赖关系的优势,成为序列转换任务中的新宠。
在 transformer 之前,主流方法是 RNN 或者 CNN,但是两者都有各自的缺点:
- RNN 通过隐藏状态可以记住所有历史,但是隐藏状态只能递归计算,无法并行化;
- CNN 可以并行计算,但是对长距离 token 之间相关性的建模能力很弱。它只能对 kernel size 内的 token 之间的相关性建模,如果需要建模长距离相关性,则必须级联很多层;
transformer 试图结合两者的优点:既能建模长距离,又能并行化。
Q:seq2seq 和 encoder-decoder 的区别:
A:seq2seq 强调目的,encoder-decoder 强调方法,seq2seq 使用的方法基本上都属于 encoder-decoder 模型。
Note
背景知识:embedding
计算机要处理任何信息都必须先将其转化成数值,比如人类可以理解的单词,但是因为每个单词有多重属性,只转化出 1 个值能表达信息的能力有限,所以一般会转成多个值,这些值组合在一起形成 1 个向量,即该 token 的向量表示 embedding vector。
Note
背景知识:attention
encoder-docoder 架构中的中间向量 C 是固定长度,所以对于长序列,压缩后的会有信息丢失,算法效果不好。attention 机制中的 encoder 编码完的结果不再是一个固定长度的中间向量 C,而是一个向量序列,这样就能解决这个问题。
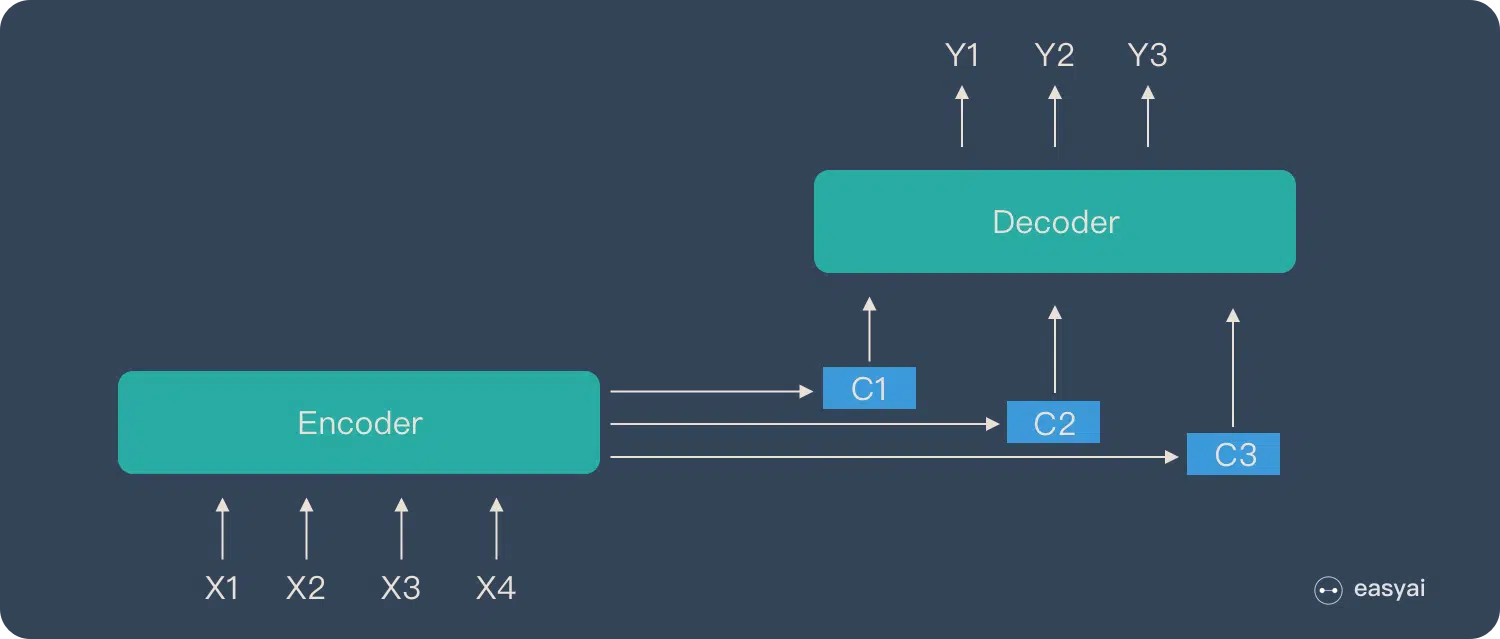
主要有两个特点:
- 没有信息丢失。
- 重要 token 和次要 token 权重不同。
attention 机制和人类处理信息的方式类似:优先关注重要信息。我们阅读一段文字时,不会平均分配注意力到每个字上面,而是会重点阅读和问题(query)相关的文字(key 和 value)。
attention 通过计算 query 和 key 的相似度,动态地调整对 input 的关注程度,所以能更有效地处理复杂任务。在数学上 attention 机制就是对 Source 中的元素的 Value 加权求和,而 Query 和 Key 用来计算对应 Value 的权重系数:
\(Attention(Query, Source) = \sum_{i=1}^{L_x}a_i * Value_i\)
其中 \(L_x\) 表示序列的长度。
\(a_i = sofmax(Sim_i) = \frac{e^{Sim_i}}{\sum_{j=1}^{L_x}e^{Sim_j}}\)
因为两个 token 对应两个向量,所以衡量两个 token 之间的相似度 \(Sim_i\) 也就变成了衡量两个向量之间的相似度。一般使用的方法有:
- cos 相似度:\(s(q, k) = \frac{q^T k}{\lvert q \rvert \cdot \lvert k \rvert}\)
- 向量点积:\(s(q, k) = q^T k\)
attention 一般分为下图的 3 个步骤:
- 第一步,query 和 key 计算相似度,得到打分 score;
- 第二步,将 score 归一化,得到每个 value 的 weight;
- 第三步,用 weight 对 value 加权求和;
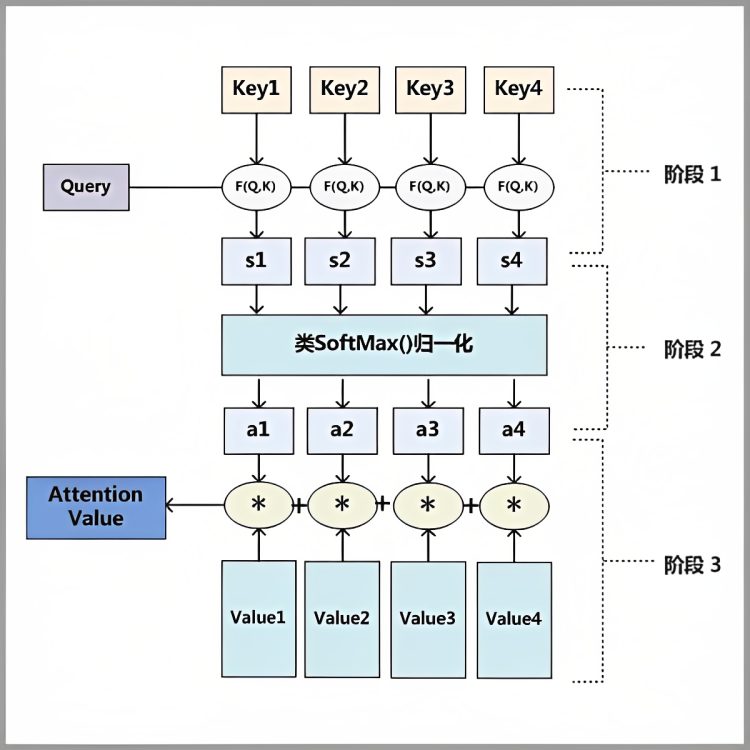
注意:上图中的 query,key,value 可以是标量,也可以是向量。
Introduction
- RNN、LSTM、特别是 Gated Recurrent Neural Network 在语言建模和机器翻译等序列建模和转换任务中已经是公认的 SOTA 方法。业界有很多方法持续扩展递归语言模型和 encoder-decoder 架构的能力边界。
- 循环模型一般沿着输入和输出进行计算,根据前一隐藏状态 \(h_{t-1}\) 和当前位置 \(t\) 计算当前隐藏状态 \(h_t\),这种递归顺序阻碍了训练的并行化。特别是在长序列中更加明显,因为有限的内存阻碍了跨样本的 batch 并行处理。
- 尽管通过 factorization trick 和 conditional computation 可以大幅提高递归模型的计算效率,在某种情况下还提高了模型性能,但是递归的顺序计算约束仍然存在。
- 在各种任务中,attention 机制已经成为序列模型和转换任务重不可或缺的组成部分,因为它可以在不考虑 sequence 中 token 的距离的情况下建立依赖关系。但是除了少数情况,大部分情况下 attention 都和循环网络结合使用。
- 本文提出一种名为
transformer的新模型架构,完全抛弃了递归网络,只依赖 attention 机制捕捉输入输出之间的全局相关性。这种架构可以有更高的并行度,只需要在 8 个 P100 上训练 12 个小时就能在翻译任务上达到 SOTA。
Backgroud
- 减少顺序计算的需求也催生了 ByteNet 和 CONVS2S 等模型,它们都采用 CNN 作为基本 block,并行计算所有输入、输出之间的 hidden representation。
- 但是这些模型中,在任意两个输入、输出位置之间建立相关性需要的操作数,会随着位置距离的增加而增加,在 ByteNet 中线性关系,在 CONVS2S 中为对数关系。所以学习远距离之间的依赖变得很困难。
- transformer 可以将这个复杂度降低为常数,但是代价是平均注意力 weight 可能会降低有效分辨率,我们通过 multihead attention 机制来克服这个问题。
- self-attention 是一种通过序列不同位置之间的相关性来计算序列 representation 的 attention 机制,应用在很多任务中。
- transformer 是第一个只依赖 attention 机制的模型。
Model Architecture
大部分序列转换 model 都基于 encoder-decoder 架构:
- encoder 把输入序列 \((x_1, x_2, \dots, x_n)\) 转化为一个连续的向量表示 \(z = (z_1, z_2, \dots, z_n)\);
- 给定 \(z\),decoder 以一次生成 1 个字符的方式生成输出序列 \((y_1, y_2, \dots, y_n)\),每一步都是自回归的,即每次都会将之前的输出也作为输入的一部分;
transformer 也遵循这样的结构,encoder 和 decoder 都基于堆叠的 self-attention 和 point-wise fc 层。
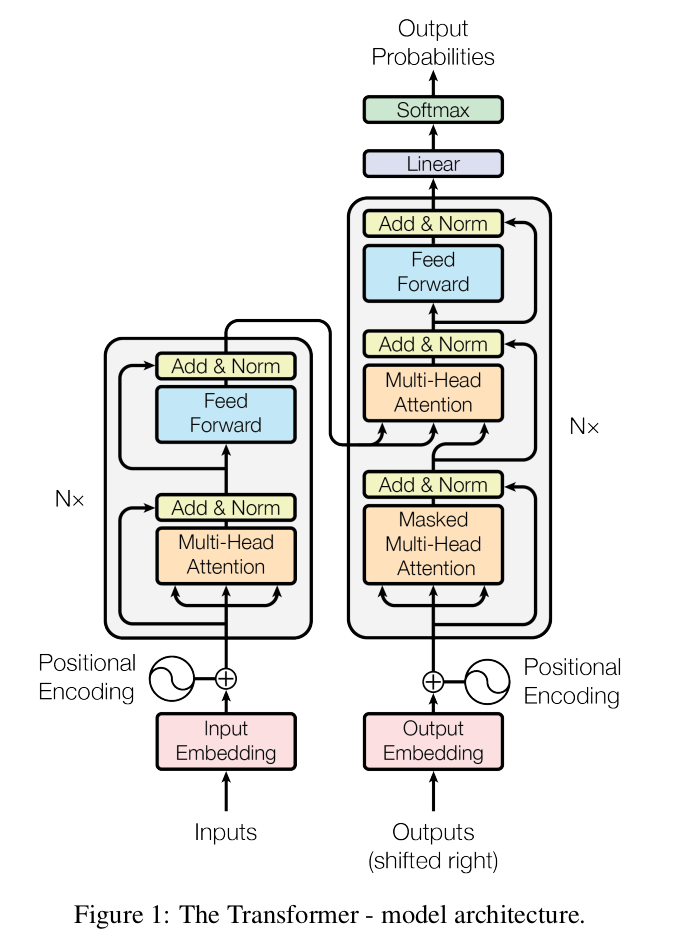
encoder and decoder stack
encoder 由 N = 6 个完全相同的 layer 堆叠组成,每个 layer 由 2 个 sub-layer 组成:
- 第一个 sub-layer 是 multi-head self-attention;
- 第二个 sub-layer 是一个简单的 point-wise fc 前馈网络;
每个 sub-layer 的输出都采用 residual 连接后接一个 layer norm 层,最终输出为 \(LayerNorm(x + sublayer(x))\),其中 \(sublayer(x)\) 为 sub-layer 本身的函数功能。
Note
- residual 的目的是防止网络退化;
- layer norm 的目的是对每一层的 activation 进行归一化;
为了实现 residual 连接,所有 sub-layer,包括 embedding 在内,输出维度均为 \(d_{model} = 512\),一般设置为训练时的最长 sequence 的 token 数量。
decoder 也由 N = 6 个完全相同的 layer 堆叠组成,除了 encoder 中的两个 sub-layer 外,decoder 中还额外插入了第三个 sub-layer,该 sub-layer 对 encoder output 做 multi-head attention 处理。
和 encoder 类似,decoder 的每个 sub-layer 也使用 residual + layer norm 连接。此外 decoder 中的 self-attention 还做了特殊设计,以防止后续位置的信息被添加到当前位置信息中,这种 mask 机制和 embedding 的偏移机制相结合,可以确保位置 i 只依赖小于 i 的已知输出,保证了 decoder 的自回归性。
Attention
attention 机制是一种将 query 和 1 组 key-value pair 映射为 output 的过程,其中 query,keys, values,output 都是 vector。
output 是 values 的加权求和,每个 value 的权重由 query 和对应的 key 的 competibility function 计算得到。
Note
本文用到 competibility function 是 dot-product。
Scaled Dot-Product Attention
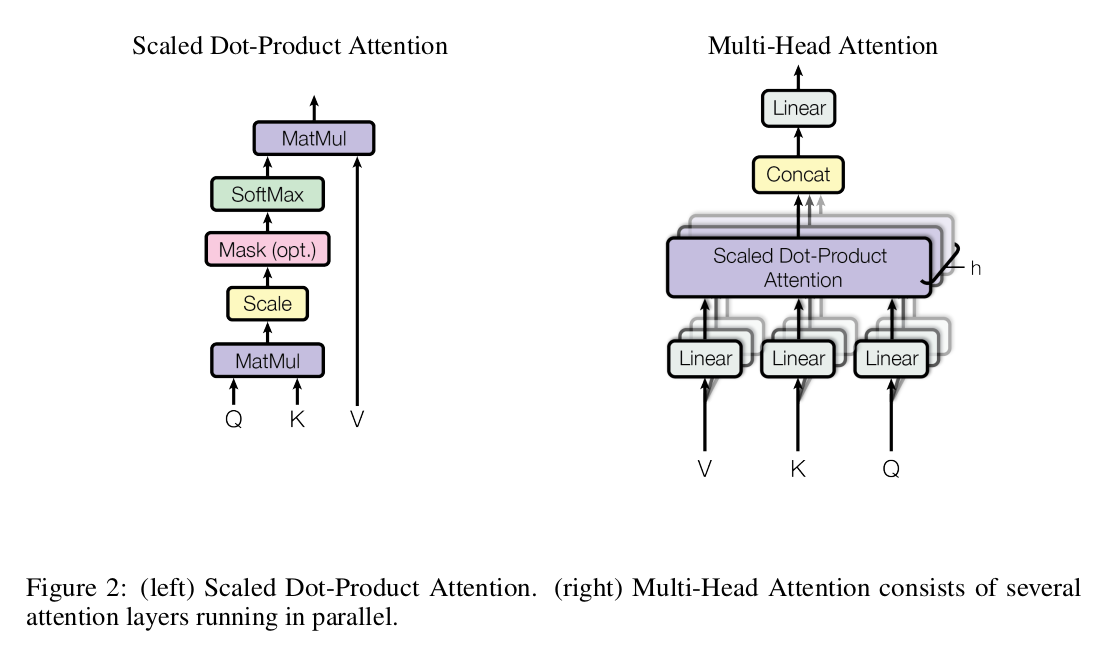
本文的 attention 叫做 scaled dot-product attention:
- 输入为 queries 和 keys,维度均为 \(d_k\);
- 计算 queries 和所有 keys 之间的点乘计算相关性,然后除以 \(\sqrt d_k\) 进行缩放;
- 然后通过 softmax 得到每个 value 的权重;
实际在 GPU 上跑时,多个 quries 打包成一个矩阵 \(Q\) 后并行计算,同理 key 和 value 也打包成矩阵 \(K\) 和 \(V\)。
\(Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt d_k}) V\)
Note
attention 的矩阵形式
第零步,输入序列被转化成 3 类数据 \(Q\),\(K\),\(V\):
输入序列一共有 n 个 token,每个 token 被 embedding 映射成 1 个维度为 \(d_{model}\) 的向量表示,则所有 token 的向量表示组合在一起形成一个矩阵 \(X \in \mathbb{R}^{n \times d_{model}}\)。
矩阵 \(X\) 分别和矩阵 \(W^Q \in \mathbb{R}^{d_{model} \times d_{model}}\),\(W^K \in \mathbb{R}^{d_{model} \times d_{model}}\),\(W^V \in \mathbb{R}^{d_{model} \times d_{model}}\) 矩阵乘得到
- \(Q \in \mathbb{R}^{n \times d_{model}}\)
- \(K \in \mathbb{R}^{n \times d_{model}}\)
- \(V \in \mathbb{R}^{n \times d_{model}}\)
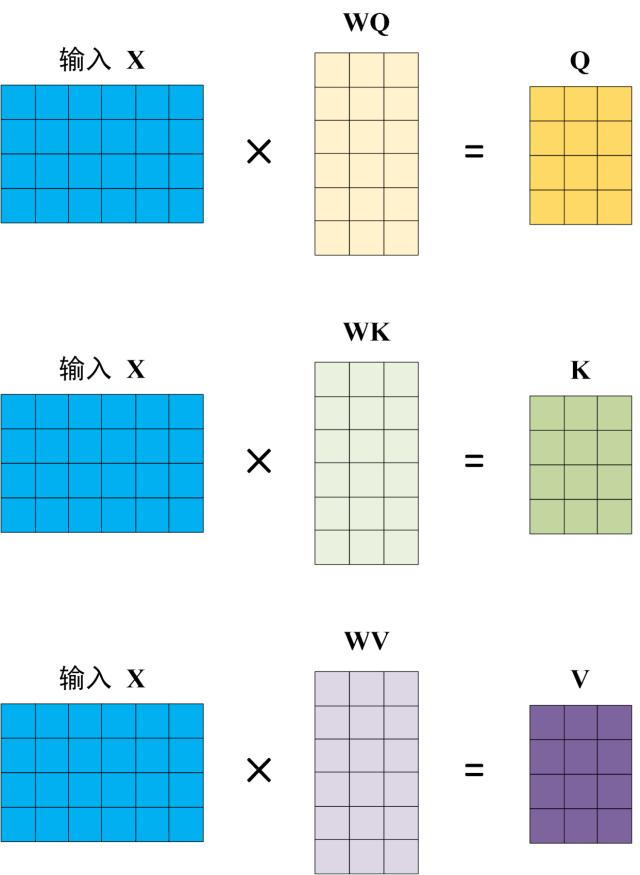
第一步,打分。计算 query 和 keys 之间的相似度,可以通过 dot-product 完成。相似度越高,说明这个 key 和 query 越相关。
\(QK^T \in \mathbb{R}^{n \times n}\),每一行的每个 element 表示该行 token 与所有 token 之间的相关性。

第二步,计算权重。将这些相似度通过 softmax 函数转化为概率权重。
sofmax 后矩阵维度不变,仍为 \(n \times n\),每 1 行对应一个 token 与其他 token 的相关性,每个行向量求和是 1。
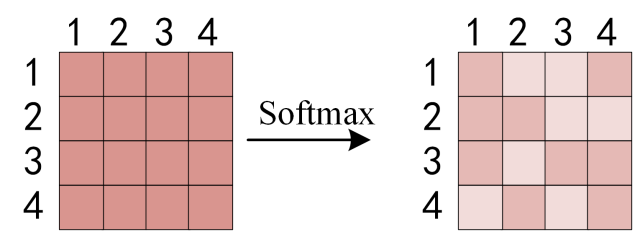
第三步,加权求和。用这些权重对所有 value 进行加权求和,相关性强的 value 向量权重大,相关性弱的 value 向量权重小。这样模型就输出了一个综合所有相关值的信息,而且突出了重要信息而忽略了不相关信息。
用每个行向量和 V 矩阵的对应行相乘,行向量的 element 广播乘 V 矩阵的行向量,如 element0 和 V 矩阵第一个行向量做广播乘,element1 和 V 矩阵第二个行向量做广播乘,依次类推。这些加权后的 value 向量之间做 elementwise 的求和,结果是一个行向量,维度为 \(1 \times d_{model}\),为输入 token 的编码输出结果。
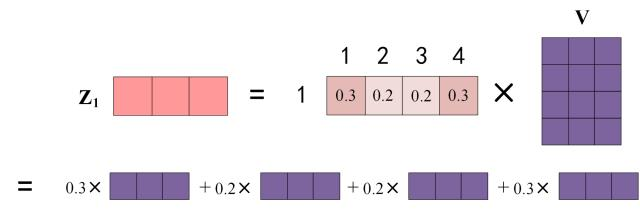
因为一共有 n 个 token,所以输出矩阵的维度为 \(n \times d_{model}\)。
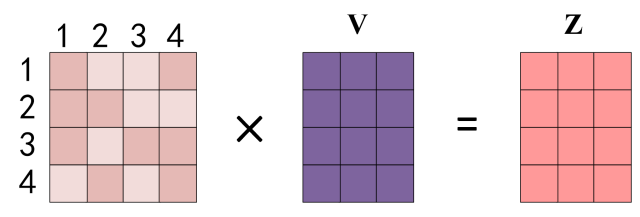
可以看出来,每个 token 的输出向量不再是独立的,而是包含了上下文信息。
最常见的 attention 有两类:
- additive attention:用一个单层的前馈网络计算兼容性;
- dot-product attention:和本文的 scaled dot-prodcut attention 相似,唯一的区别是不包含除以缩放因子 \(\sqrt d_k\) 的步骤;
尽管两种 attention 的计算量相同,但是 dot-product attention 要快得多,空间效率也更高,因为它可以利用高度优化的矩阵乘代码加速。
Q:为什么需要缩放因子?
A:当 \(d_k\) 很大时,点积的幅值会很大,导致 softmax 的梯度非常小,所以需要除以 \(\sqrt d_k\)。
Note
比如 q 和 k 都是均值为 0,方差为 1 的向量,则它们的点积的均值为 0,方差为 \(d_k\),为了抵消这种影响,需要将点积缩放 \(\frac{1}{\sqrt d_k}\) 倍。
Multi-Head Attention
相比于维度为 \(d_{model}\) 的单头 attention,multi-head 能更有效地捕捉信息,因为 multi-head 能同时关注到不同位置的多种特征信息,相比之下只有一个 head 则平均化了这些信息,从而限制了模型的表达能力。
multi-head attention 算法过程:
- 把 queries,keys,values 分别 linear projection 映射 h 次,每次用不同的学习到的参数,且每次映射后的 queries,keys,values 的维度缩小为 \(d_k\),\(d_k\),\(d_v\)。
- 在每次映射后的 queries,keys,values 版本上的计算 attention,每次产生 \(d_v\) 维的 output;
- 将这些 output concat 到一起后再做一次 linear projection,得到最终 output;
\(MultiHead(Q, K, V) = Concat(head_1, head_2, \dots, head_h)W^O\)
\(head_i = Attention(QW_i^Q, KW_i^K, VW_i^V)\)
其中,
\(W^Q \in \mathbb{R}^{d_{model} \times d_k}\)
\(W^K \in \mathbb{R}^{d_{model} \times d_k}\)
\(W^V \in \mathbb{R}^{d_{model} \times d_v}\)
\(W^O \in \mathbb{R}^{hd_v \times d_{model}}\)
在本文中 \(h = 8\),\(d_k = d_v = d_{model}/h = 64\),因为每个 head 的维度都变小了,所以总计算量和单一 attention 近似相同。
Note
从 \(W^Q\),\(W^K\),\(W^V\),\(W^O\) 的维度可以看出来,multi-head 就是将单 head 的大维度 \(d_{model}\) 等分成了 h 份,分别算出各自的 attention output 后重新 concat 到一起恢复出原来的大维度。
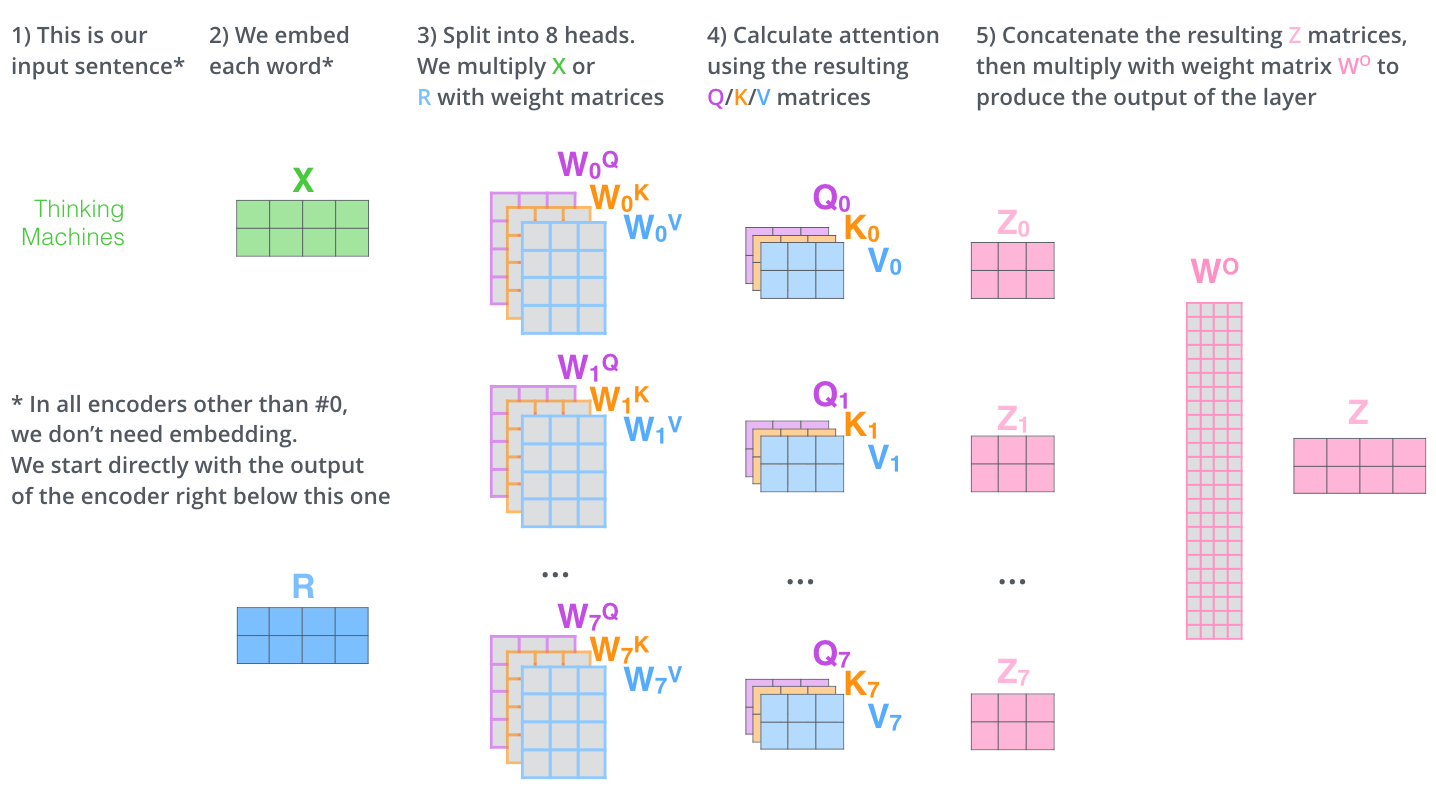
Multi-head Attention in Model
transformer 以 3 种方式应用 multi-head attention:
- encoder-decoder attention:queries 来自前一个 decoder layer,而 keys 和 values 来自 encoder output,这样使得 decoder 的每个位置都能关注到所有输入位置。
- encoder 中的 self-attention:所有的 queries,keys 和 values 都来自同一个地方 —— 前一个 encoder layer 的输出。encoder layer 中的每个位置都能关注到前一个 attention layer 的所有位置。
- decoder 中的 self-attention:所有位置都能关注到当前位置及以前位置,为了保持 decoder 的自回归性,需要阻止 decoder 中的信息向左流动。具体是通过 mask 将 softmax 的非法输入的值改为 \(-\infty\) 来实现。
Note
一般的 encoder-decoder 架构中 source 和 target 不同,attention 发生在 target 的 query 和 source 的所有 key,value 之间,而 self-attention 发生在 source 内部,或者 target 内部。
单个 output token 的产生过程:
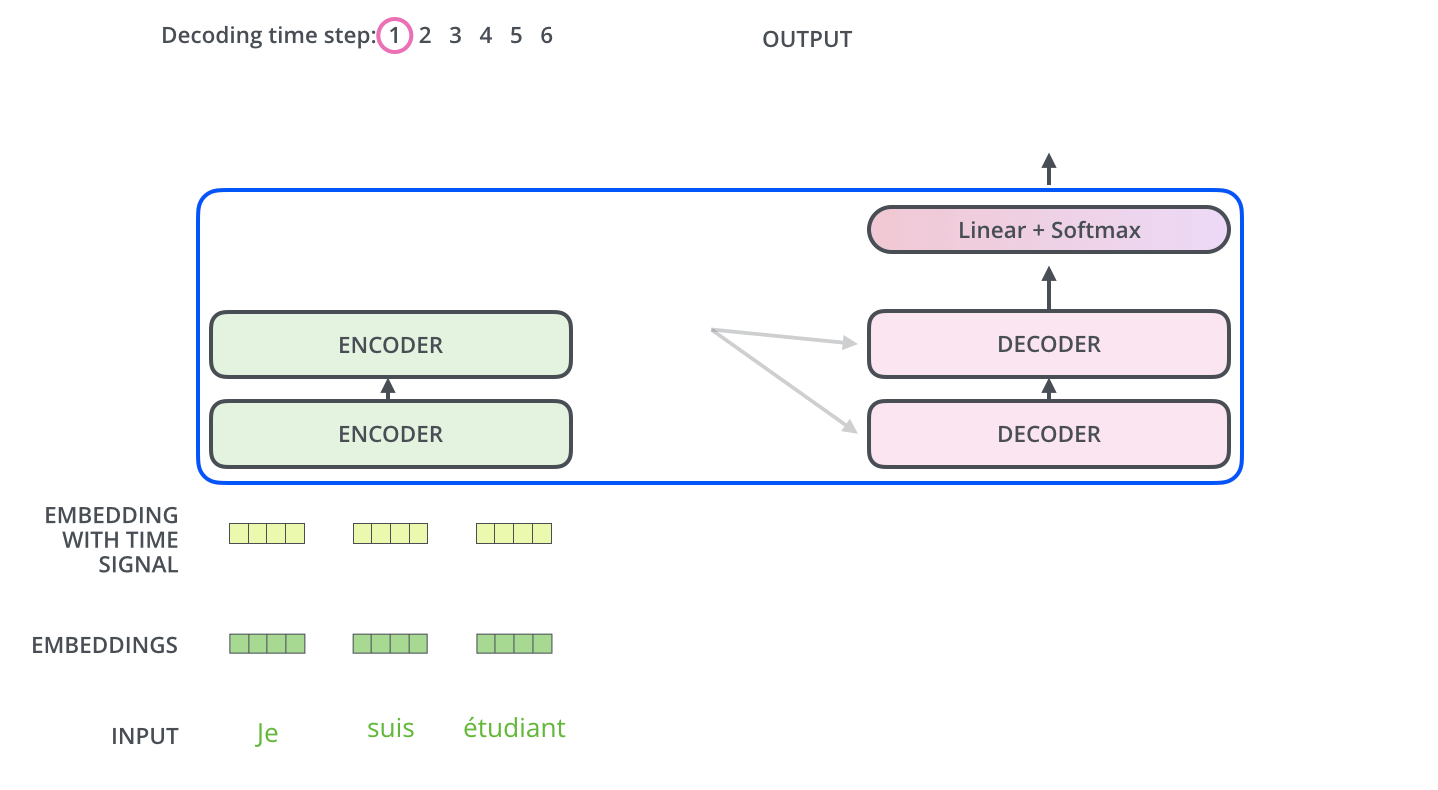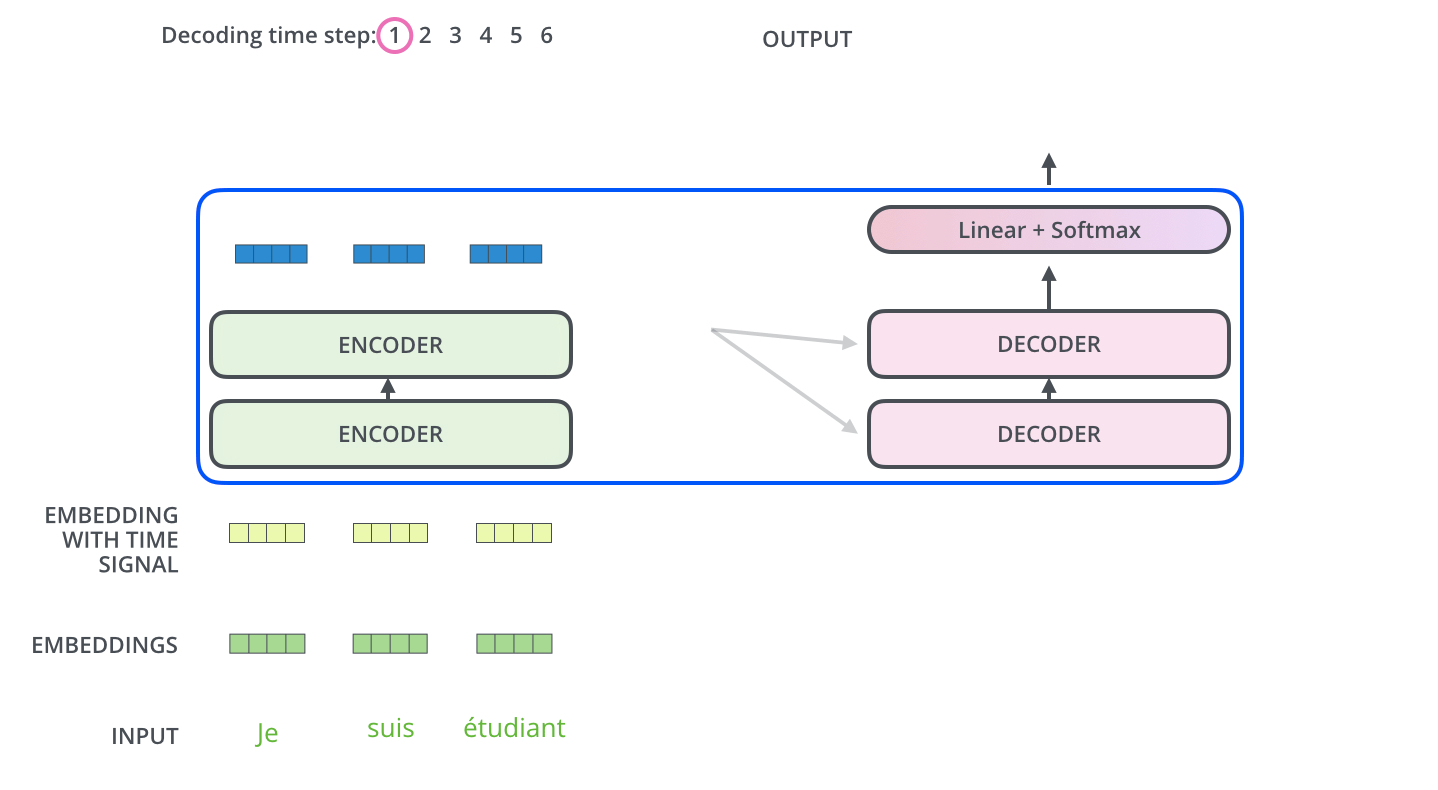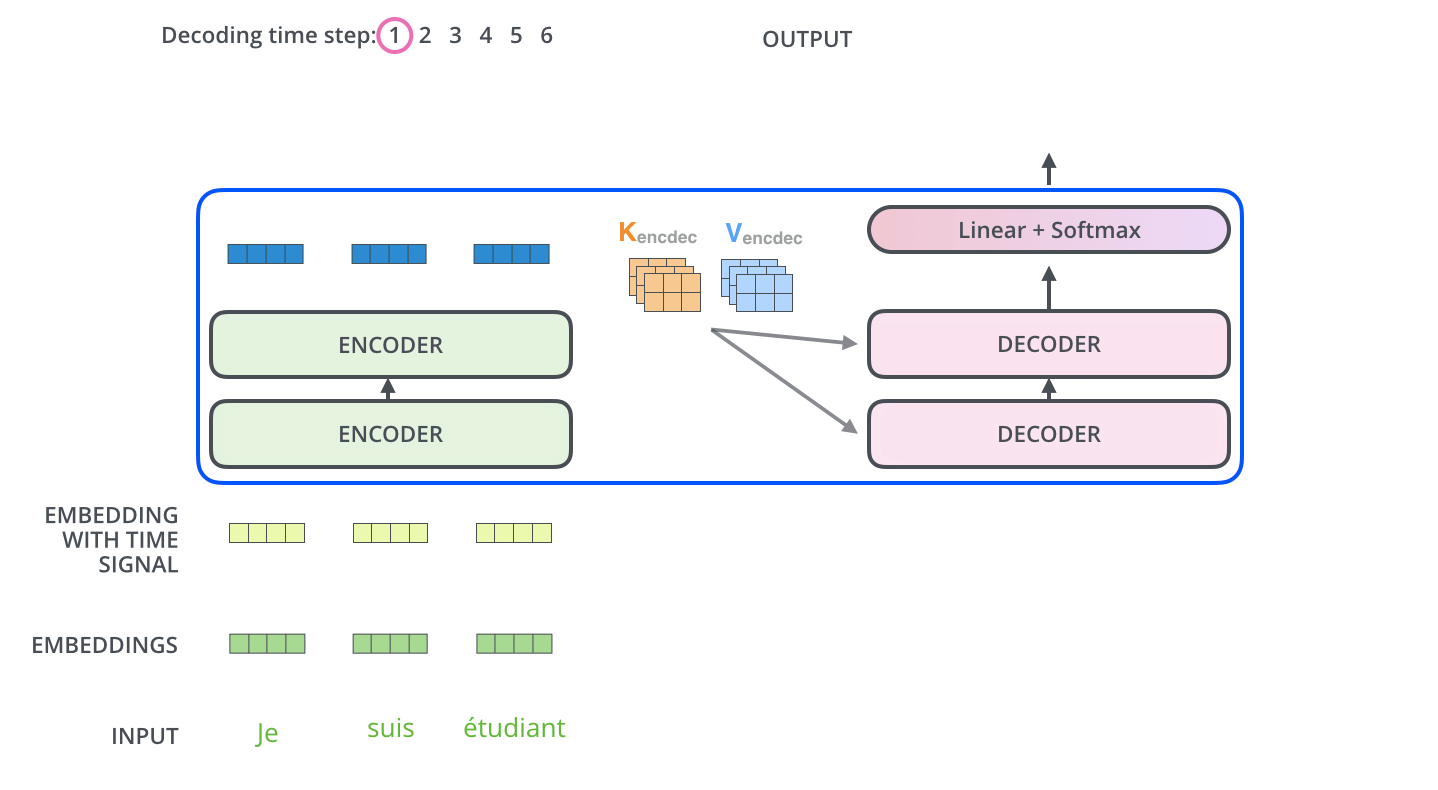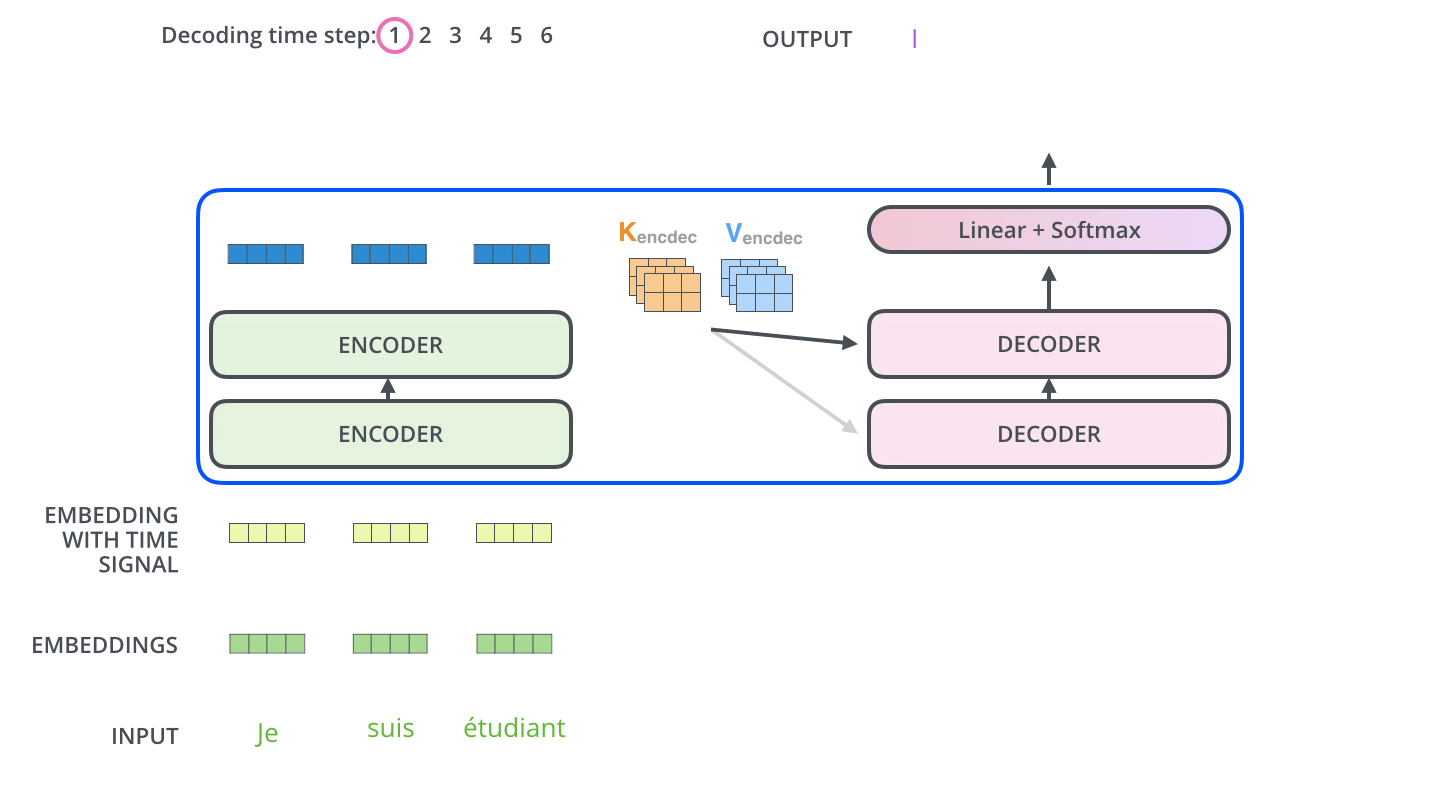
多个 output token 自回归过程:
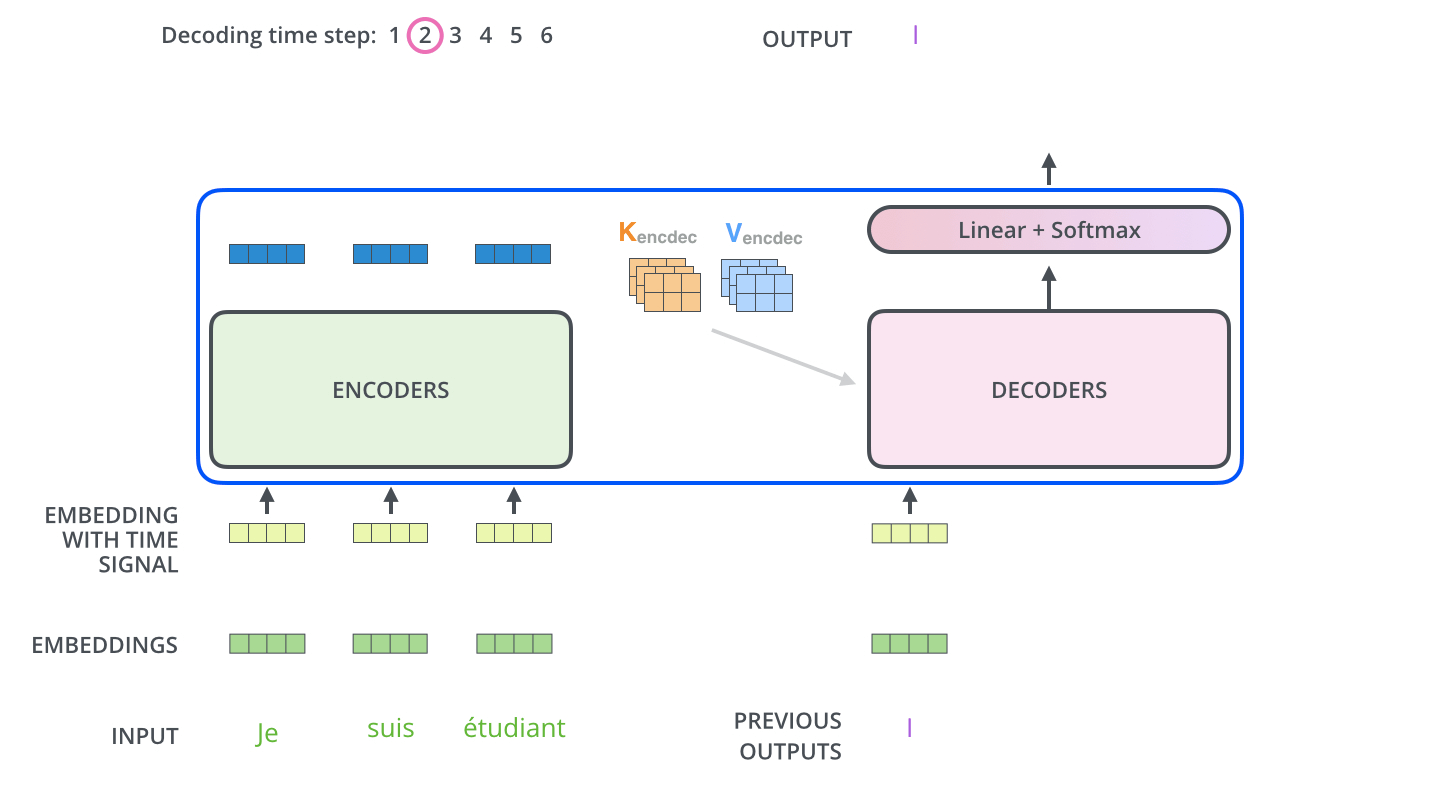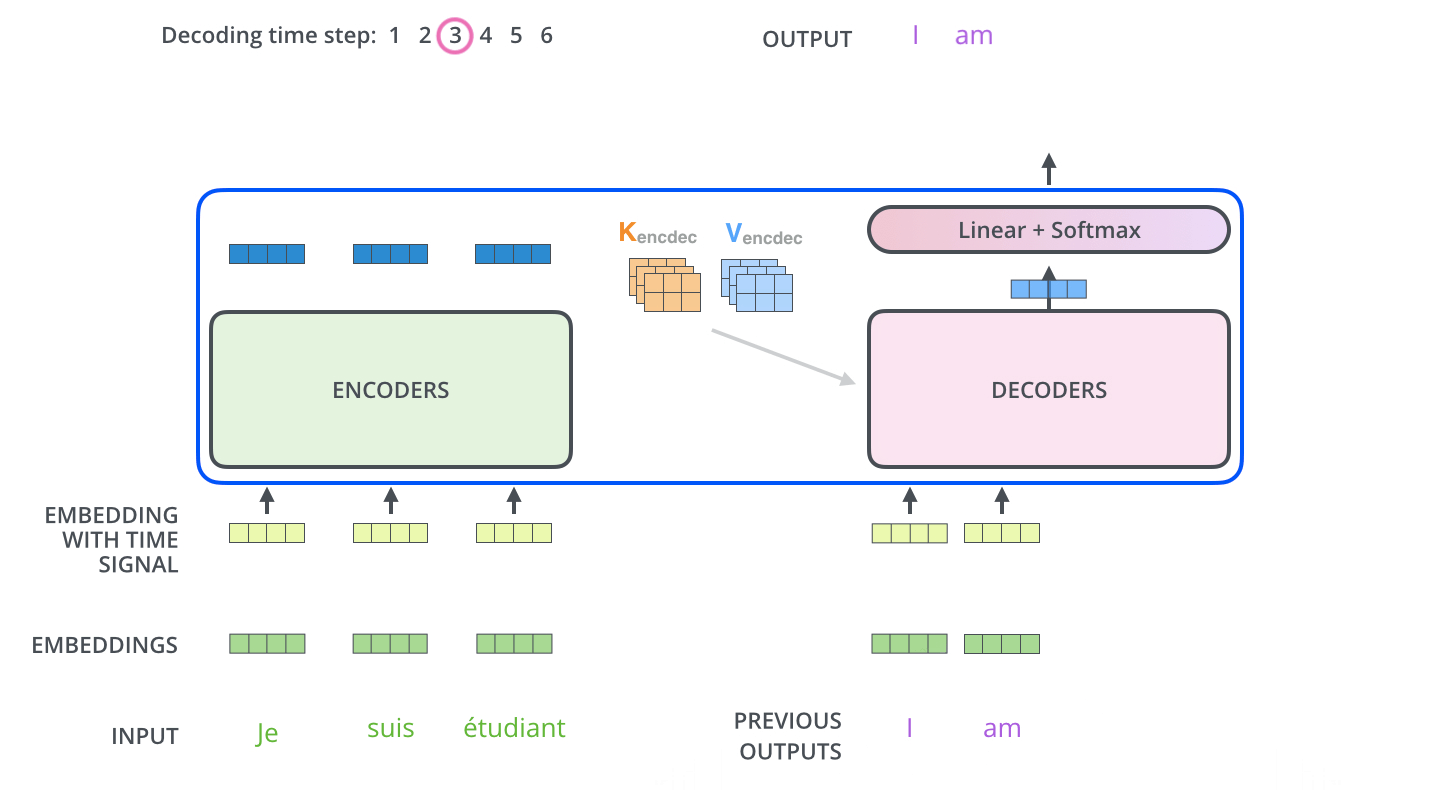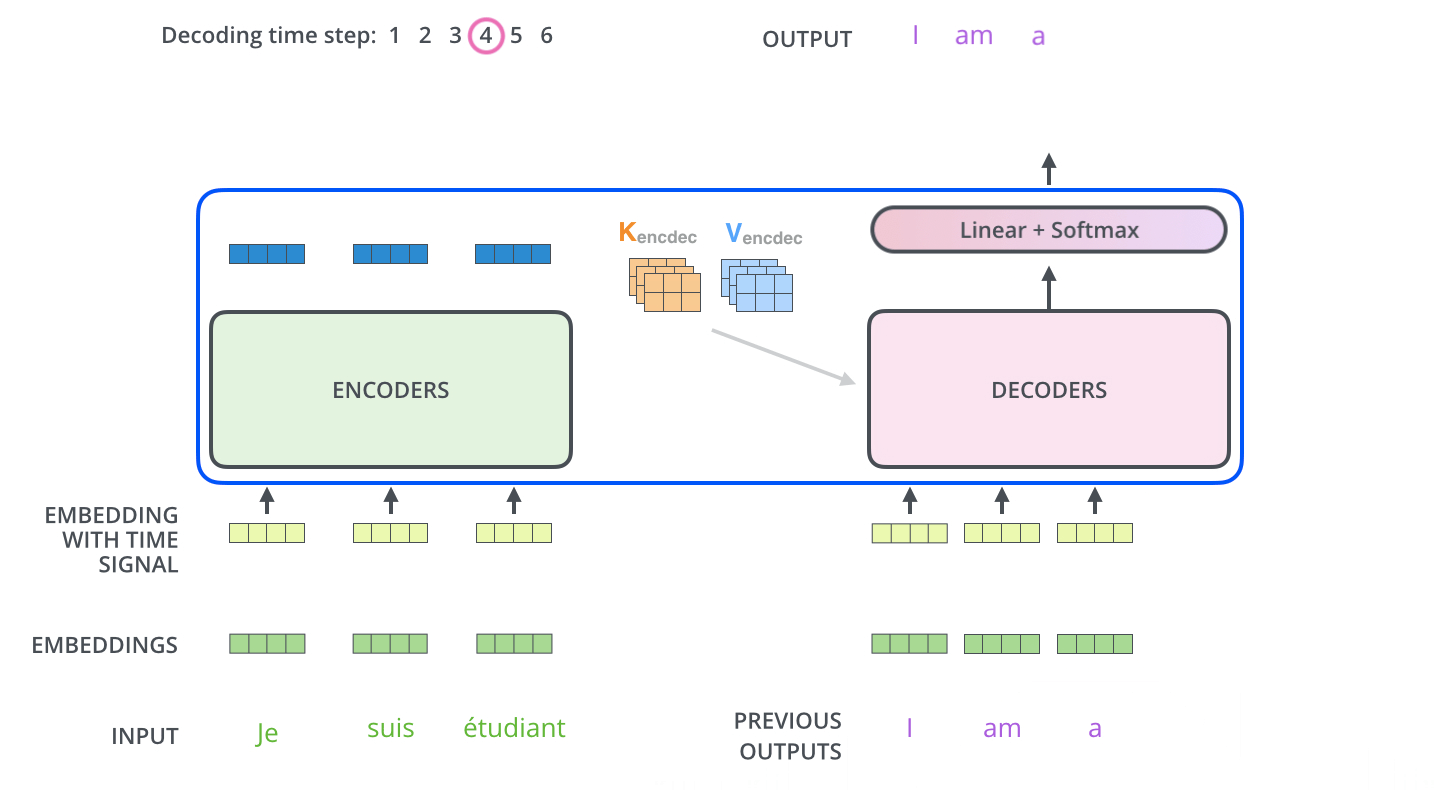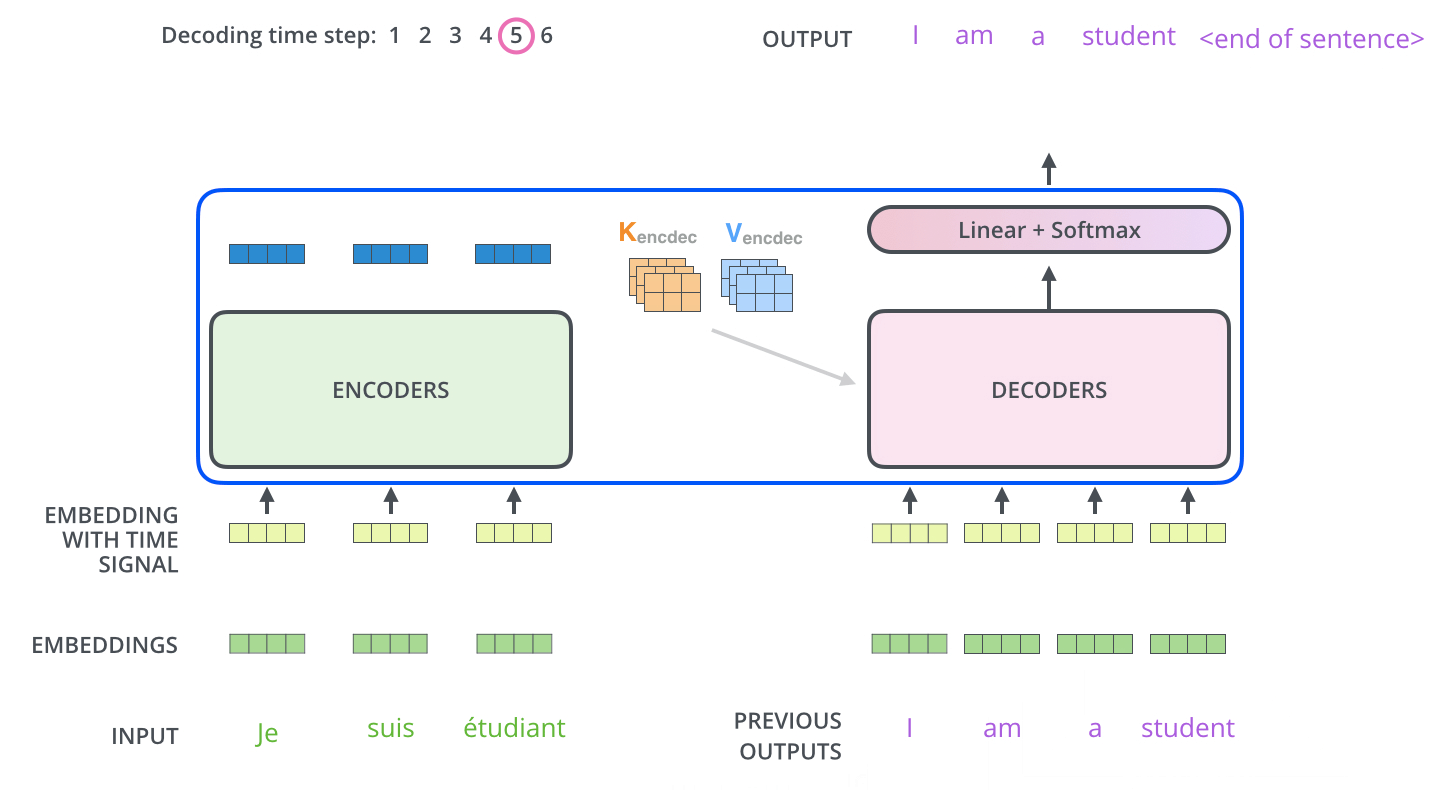
Note
encoder stack 的最终输出是 K,V 矩阵,用于每个 decoder 的 encoder-decoder attention。所有 encoder 只在训练时有用,推理时只需要 decoder 就足够了。
Q:decoder attention 仍然是 attention,每次输出一个 token 对应的一个维度为 \(1 \times d_{model}\) 的向量,如何从这个向量得到输出 token?
A:linear + softmax。
首先 linear,即 fc 层,将 decoder 的输出 vector 映射为一个非常非常大的 logits vector,该 vector 的维度即 model 的字典大小,每个值表示对应字的 score。
其次,softmax 将每个 score 转化为概率,然后选择概率最大的字输出。
Point-wise Feed-Forward Networks
每个 encoder layer 和 decoder layer 中除了 attention sub-layer 之外,还包含一个 FFN。该网络结构为两个线性变换中间插入了一个 ReLU。
\(FFN(x) = max(0, xW_1 + b_1)W_2 + b_2\)
虽然所有位置都使用相同的线性变换公式,但是每层不同位置的 weight 都不同,所以这个线性变换也可以当成是 k=1 的 convolution。
输入、输出的 \(d_{model} = 512\),中间层的维度为 \(d_{ff} = 2048\)。
Embedding and Softmax
和其他序列转换模型类似,本文也通过 learned embedding 将输入、输出 token 映射成维度为 \(d_{model}\) 的 vector。
本文也使用常见的基于 learned linear transformation 和 softmax 将 decoder 的输出转化为下一个 token 出现的概率。
在我们的模型中,两个 embedding layer 和 pre-softmax linear transformation 共享相同的 weight,其中 embedding layers 给 weight 乘以 \(\sqrt{d_{model}}\) 进行了缩放。
Positional Embedding
因为网络中没有 RNN 和 CNN,所以为了建模序列的顺序信息,必须注入序列中 token 的相对和绝对位置信息,具体方法是:
将 positional embedding 添加到 encoder 和 decoder 的 embedding layer 中,而且 positional embedding 的维度也为 \(d_{model}\),以便两者可以求和。
positional embedding 的方法有很多种(学习到的 or 固定参数的),本文使用的方法是不同频率的 sin 和 cos 函数:
\(PE_{(pos, 2i)} = sin(pos/1000^{2i/d_{model}})\)
\(PE_{(pos, 2i+1)} = cos(pos/1000^{2i/d_{model}})\)
其中 \(pos\) 为 position,\(i\) 为 dimension。即 position embedding 的每个维度都是一个 sin 曲线。
Note
选择 sin 曲线的好处:
- sin 函数是一个周期函数,当 sequence 变得比训练 sequence 更长时也能算出来;
- 可以很容易地根据相对位置算出 positional embedding:\(sin(A+B) = sin(A)cos(B) + cos(A)sin(B)\);
Note
positional embedding 的值是直接 element-wise 加到 embedding 的值上面的,而不是 concat。
试验表明 learned 方式效果相同,但是我们选择了 sin 函数的版本,因为它使模型更能适应比训练更长的序列。
Why Self-Attention
本文对比了 self-attention layer 和其他序列转换 encoder-decoder 中常见的 RNN/CNN layer,基于以下 3 点考虑最终选择了 self-attention。
- 每层的计算量;
- 可并行计算的比例,通过所需的最小顺序计算量来衡量;
- 网络中 long-range dependencies 之间的 path-length(序列转换中的关键挑战,path-length 越短模型学习 long-range dependencies 的能力越强);

对于第二点顺序计算量:
self-attention 连接了任意两个位置,所以任意两个位置之间相关性的顺序计算量为常数 O(1) ,即只需要一步就可以得到,而 RNN 需要迭代 O(n) 次顺序操作才能得到;
对于第一点计算量:
当序列长度 n < 表示维度 d 时,self-attention 比 RNN 更快。一般来说都满足这个条件。对于很长的序列,则 self-attention 不如 RNN,但是这个问题可以通过限制 self-attention 的半径来解决。
kernel 大小 k < n 的 conv 无法连接所有的 input-ouput pair,如果要实现这个目标,需要级联 O(n/k) 个 conv 或者 \(O(log_k(n))\) 个 dilated conv。一般来说 conv 的复杂度约为 RNN 的 k 倍。separable conv 可以降低复杂度到 \(O(k \cdot n \cdot d + n \cdot k^2)\),当 n = k 时,它的复杂度和本文所用的 self-attention + point-wise forward layer 相同。
self-attention 的另外一个好处是模型更加可解释,不仅每个 head 学习到不同的任务,多个 head 还表现出和句子语法和语义相关的行为。
Result
- 单一 head 比 multi-head 差;
- head 数量过多也会变差;
- 减小 \(d_k\) 会损害效果,设计比点积更复杂的 competibility function 可能是有益的;
- 更大的模型一般效果更好;
Conclusion
本文提出了 transformer 网络:
- 第一个完全基于 attention 的序列转换模型,用 multi-head self-attention 代替传统 encoder-decoder 中的 recurrent layer;
- 对于翻译任务,transformer 的训练速度明显比其他基于 RNN 和 CNN 的模型更快,翻译效果 SOTA;
- 计划将 transformer 扩展到除 text 之外其他模态的应用中;
- 计划研究 local,restricted transformer 来处理大数据量的 input/output,比如 image,audio,video;
- 另外一个研究目标:让生成过程尽量避免顺序执行;