流水线 pipeline 的艺术

Posted on 2015-05-19 00:00 in IC

pipeline

PC 世界永恒不变的信条就是提高性能，其中一个方法就是提高系统的时钟频率。

在另外一篇 blog 静态时序分析 STA 中已经总结过了，限制系统最大工作频率的因素有很多，设计者能够控制的是 DFF 之间的组合逻辑的时延 Tcomb，降低最大时延路径（关键路径，critical path）的时延 Tcomb，就可以提高系统的工作频率。

如何降低呢？方法就是流水线（pipeline）。

Pipeline Intro

所谓流水线（pipeline）设计，应该是从汽车工业中的 流水生产线 借鉴过来的说法吧。

在汽车生产的时候，假设分为 5 个阶段，每个阶段都需要 1 个工人花费 1 小时完成，因为后续的阶段必须等前面阶段完成后才能进行，所以总共需要 5 个小时才能完成一辆汽车。但是采用流水线方式，在进行后续阶段时，前面的阶段可以进行新的工作，那么每个小时都可以生产出一辆汽车了，生产效率提高了 5 倍。

可以看到，流水线之所以可以大大提高效率的原因在于：传统的方式，某个阶段进行时，其他阶段是空闲等待的，浪费时间；而流水方式中，在处理后续阶段时，前面的阶段可以进行新的加工，每时每刻，每个工人都是在工作的，这就是流水线能提高生产效率的原因。

和汽车生产类似，组合逻辑路径可以看作是一条生产线，路径上的每个逻辑单元都可以看作是一个阶段，都会产生时延。

  • 如果不采用流水设计，前后级组合逻辑依次工作，那么这条路径的模型就是原始的生产线

  • 如果采用流水设计，那么前后级组合逻辑可以同时工作，就像新的生产线一样

A Simple Example

采用流水设计的方法就是：在较长的组合逻辑路径中插入 DFF，将其分割为几个小的组合逻辑，新的 Tcomb 显然小于原来的 Tcomb，所以系统的时钟频率就可以提高了。

举例来说明：设计一个电路完成 i = (a + b + c + d) + (e + f + g + h) 运算。

下面是没有流水的设计：

no-pipe

可以计算出第一级 DFF 到第二级 DFF 之间数据路径的时延为 

Tff = Tco + Tcomb
    = Tco + 3*Tadder

下面是插入两级流水的设计：

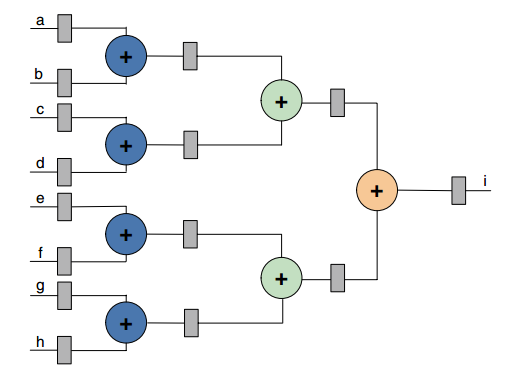
piple

现在相邻的两级 DFF 之间的组合逻辑只有 1 级加法器，而不是原来的 3 级，这时数据路径的时延为

Tff = Tco + Tcomb
    = Tco + Tadder

显然，采用流水后 Tff 更小，系统能够达到的工作时钟频率也就更高。

Performance Increase from Pipelining

下面更加详细地分析一下流水带来的速度性能的提升。

首先说明，可以使用系统的流量 throughout 和系统的时滞 latency 来衡量速度性能。

  • throughout: 每个时钟周期处理的数据量，单位一般是 bps

  • latency: 数据输入到数据输出之间的时间，一般用 时钟周期的个数 来表示

如下图所示，两个 DFF 之间存在着大规模的组合逻辑：

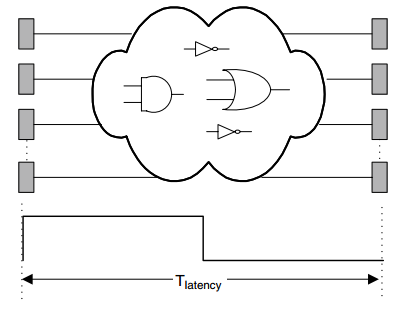
before

组合逻辑的时延决定了系统的最大工作频率（也即时钟周期 T 的最小值），此时

latency = Tcomb + Treg + Tclk               -- Eq1
Tbefore = latency = Tcomb + Treg + Tclk     -- Eq2

其中 Treg 表示 DFF 带来的时延，Tclk 表示时钟的 skew 和 jitter 带来的时延。

在使用流水之后，如下图所示：

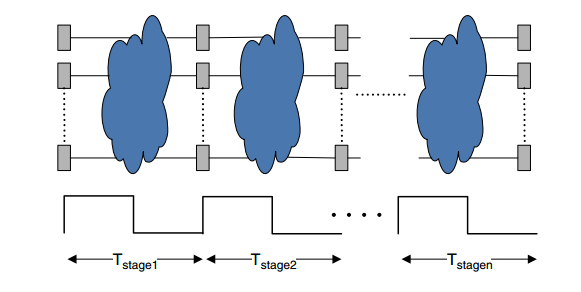
after

此时，每个 stage 的周期为

Tstage = (Tcomb)stage + Treg + Tclk

而时延最大的那个 stage 决定了系统的最大工作频率（也即时钟周期 Tclk 的最小值），此时

Tpipe = max{(Tcomb)stage} + Treg + Tclk

latency = n * Tpipe

在理想状况下，各 stage 的时延应该相等，从而达到最小的 latency。即

Tcombi = Tcomb / n

所以，最小的流水周期 Tpipe 为

(Tpipe)min = Tcomb / n + Treg + Tclk

代入 latency 的表达式，有

latency = n * (Tpipe)min
        = Tcomb + n(Treg + Tclk)                -- Eq3

Tafter  = Tpipe = Tcomb / n + Treg + Tclk       -- Eq4

首先比较系统的工作频率，或者 throughout（Eq2 和 Eq4）：

Fafter / Fbefore = Tbefore / Tafter
                 = (Tcomb + Treg + Tclk) / (Tcomb/n + Treg + Tclk)

显然这个数 > 1，即

conclusion: 系统的工作频率和 throughout 得到了提升。

如果定义 k = (Treg + Tclk) / (Tcomb + Treg + Tclk)，为 reg 和 clk 占的总周期的比例，则

Fafter / Fbefore = 1 / [(1-k/n) + k]

其次，比较 latency（Eq1 和 Eq3）：

Lafter / Lbefore = [Tcomb + n(Treg + Tclk)] / (Tcomb + Treg + Tclk)

显然这个数 > 1，即

conclusion: 系统的 latency 增加了（增加的很小，近似可以忽略）。

最后比较面积：

conclusion: 使用流水比不使用流水多使用了 n * m 个 DFF，还使用了更多的连线资源。

综上，可以看到，虽然流水可以提高系统的工作频率和吞吐率，但是它付出的代价是面积和功耗的增加，这也是速度和面积之间相互转化的体现。

DXL Instruction

THE ART OF HARDWARE ARCHITECTURE 中还介绍了 DXL 指令集的实现，简单记录一下笔记，详细过程还是看书吧。

DXL 指令是 32 位的 RISC 微处理器，每条指令最多由 5 个部分组成：

  1. Instruction Fetch (IF)

  2. Instruction Decode/Register Fetch (ID)

  3. Execution/Effective address cycle (EX)

  4. Memory access/branch completion cycle (MEM)

  5. Write Back Cycle (WB)

非流水的方式实现如下图：

dxl nopipe

因为是非流水的方式，所以指令不能并行执行，必须等到前一条指令执行完之后才能开始执行下一条指令，如下图所示，假设每条指令需要 8 ns，那么执行 4 条指令总共需要 8 * 4 = 32 ns。

dxl order1

采用流水的方式，在 5 级操作中都加上一个流水阶段（即每个阶段加入一组 DFF），实现如下图：

dxl pipeline

因为是流水的方式，所以指令可以并行执行，如下图所示：

dxl order2

假设执行每条指令花费 10 ns，那么执行 5 条指令：

非流水的方式总共花费 10 * 5 = 50 ns；流水的方式每条指令花费 5 个时钟周期，每个周期只有 2 ns，完成 5 条指令只需要 5 个时钟周期，总共花费 9 * 2 = 18 ns；性能是原来的 50/18 = 2.8 倍。

Pipelining Principles

THE ART OF HARDWARE ARCHITECTURE 还总结了流水需要注意的问题：

  1. 所有的中间值必须在各周期锁存

  2. 不能复用任何模块

  3. 一个阶段的所有操作必须在一个周期内完成

  4. 冒险会给流水带来问题，冒险分为

    1. 结构冒险，由于资源不够，无法同时支持所有指令同时执行

    2. 数据冒险，执行需要的中间数据还没有计算出来

    3. 控制冒险，分支点流水线和其他指令改变程序的计数器的值

    解决以上问题的方法就是停止流水线直至风险解除，在流水线中插入多个 “ 气泡 ”（缺口）。

Another Example

将前面总结的 “ 在组合逻辑路径中插入 DFF，形成流水 ” 的思路进一步扩展，可以得到更加上层的流水思想。Advanced FPGA Design: Architecture, Implementation, and Optimization 中介绍了一个算法中使用流水的例子，其关键在于 “ 拆开环路 ”：

假设要计算 x^3 这个值，下面这段软件的代码

Xpower = 1;
for (i = 0; i < 3; i++)
    Xpower = X * Xpower;

将这段软件代码翻译成 Verilog 代码，重复使用相同的寄存器和计算资源，得到的结果如下：

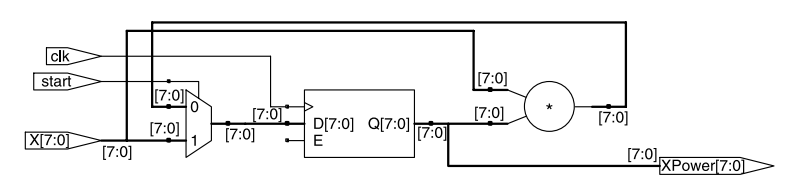
iterative

这种迭代的方法无法实现并行计算，其性能：

Throughput = 8 /1, or 8 bits /clock
Latency = 3 clocks
Timing = One multiplier delay in the critical path

而使用 pipeline 的方法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
// stage 1
X1 <= X;
Xpower1 <= X;

// stage 2
X2 <= X1;
Xpower2 <= Xpower1 * X1;

// stage 3
Xpower <= Xpower2 * X2;

得到的结果如下图：

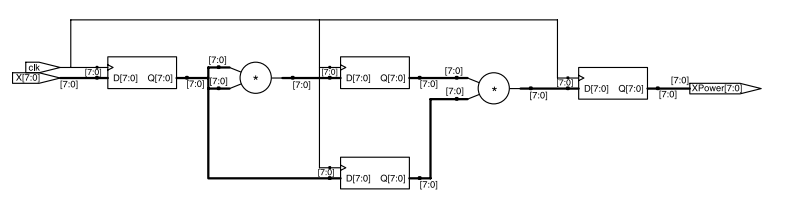
pipeline

可以并行计算，其性能：

Throughput = 8 bits / clock (assuming one new input per clock)
Latency = Betw een one and two multiplier delays, 0 clocks
Timing = Two multiplier delays in the critical path

可以看到，throughout 的提升是以面积为代价的。

Ref

THE ART OF HARDWARE ARCHITECTURE

Advanced FPGA Design: Architecture, Implementation, and Optimization

Previous Post Next Post