相关系数及Matlab函数

Correlation

首先总结一下基础背景知识：

相关 Correlation 是概率论与统计学中用来刻画两个随机变量之间统计关系的强弱和方向的量。在广义的定义下，有很多种类的相关系数（correlation coefficient），它们通常用字母 ρ 或者 r 来表示。

我们通常说的相关系数的学名是：皮尔逊积差系数（Pearson's product moment coefficient），这种相关系数只对两个变量的线性关系敏感。

Pearson's product moment coefficient

在统计学中，基于总体的定义如下：

Pearson 相关系数使用两个变量的协方差（covariance）和标准差（standard deviations）来定义：

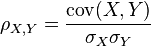
其中，cov 是协方差，sigma 是标准差。因为 cov 可以写作：

所以 Person 相关系数的定义式可以写作：

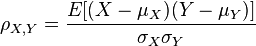
根据概率论知识可以得到如下的变形形式：

基于样本来估计协方差和标准差，可以得到定义如下：

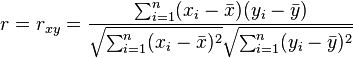
通过变形，可以得到下式：

Properties

wiki:

当两个变量的标准差都不为零，相关系数才有定义。从柯西 - 施瓦茨不等式可知，相关系数的绝对值不超过 1。当两个变量的线性关系增强时，相关系数趋于 1 或 -1。当一个变量增加而另一变量也增加时，相关系数大于 0。当一个变量的增加而另一变量减少时，相关系数小于 0。当两个变量独立时，相关系数为 0. 但反之并不成立。这是因为相关系数仅仅反映了两个变量之间是否线性相关。比如说，X 是区间［－1，1］上的一个均匀分布的随机变量。Y = X2. 那么 Y 是完全由 X 确定。因此 Y 和 X 是不独立的。但是相关系数为 0。或者说他们是不相关的。当 Y 和 X 服从联合正态分布时，其相互独立和不相关是等价的。

当一个或两个变量带有测量误差时，他们的相关性就受到削弱，这时，“ 反衰减 ” 性（disattenuation）是一个更准确的系数。

【总结】matlab 求两个序列的相关性

相关系数只是一个比率，不是等单位量度，无什么单位名称，也不是相关的百分数，一般取小数点后两位来表示。相关系数的正负号只表示相关的方向，绝对值表示相关的程度。因为不是等单位的度量，因而不能说相关系数 0.7 是 0.35 两倍，只能说相关系数为 0.7 的二列变量相关程度比相关系数为 0.35 的二列变量相关程度更为密切和更高。也不能说相关系数从 0.70 到 0.80 与相关系数从 0.30 到 0.40 增加的程度一样大。

对于相关系数的大小所表示的意义目前在统计学界尚不一致，但通常按下是这样认为的：

相关系数 相关程度

0.00-±0.30 微相关

±0.30-±0.50 实相关

±0.50-±0.80 显著相关

±0.80-±1.00 高度相关

复习了基础知识，另外还有两个概念：

Cross-correlation

对于连续函数，有下面的定义：

对于离散函数，有下面的定义：

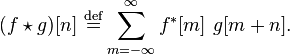
在信号处理中，用 互相关 Cross-correlation 来衡量两个序列之间的相似程度，通常可以用于在长序列中寻找一个特定的短序列（也就是通信系统的同步中）。

在数理统计中，互相关用来两个随机序列的相关性。

从定义式中可以看到，互相关函数和卷积运算类似，也是两个序列滑动相乘，但是区别在于：

互相关的两个序列都不翻转，直接滑动相乘，求和；卷积的其中一个序列需要先翻转，然后滑动相乘，求和。

所以，f(t) 和 g(t) 做相关 = f*(-t) 与 g(t) 做卷积

Autocorrelation

自相关 Autocorrelation 是互相关的一种特殊情况，就是一个序列和它本身做相关，而不是两个序列，它主要用来衡量一个序列在不同时刻取值的相似程度。

在数理统计中，自相关的定义式如下：

如果随机过程是一个宽平稳过程，那么均值和方差都不是时间的函数，所以，自相关定义式变为：

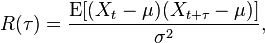
在某些学科中，会去掉归一化因子 σ2，使用 自协方差 来代替 自相关。但是归一化因子可以让自相关的取值在 [-1, +1] 之间，不会随着序列的绝对大小而变化。

在信号处理中，

自相关的定义会去掉归一化，即不用减去均值，也不用除以方差。当除以方差时，一般叫做另外一个名字：自相关系数 autocorrelation coefficient。

对于连续函数，自相关的定义如下：

对于离散函数，自相关的定义如下：

自相关有很多性质，比如对称性、维纳 - 辛钦定理（Wiener–Khinchin theorem） 等，就不再重复了。

Matlab function

xcorr

在 Matlab 中，计算自相关和互相关，可以使用同一个函数：xcorr。

自相关：

c = xcorr(x);

互相关：

c = xcorr(x, y);

因为两个长度为 N 的序列进行相关，可以知道最多有 2N - 1 个非 0 的移位相乘结果，所以 xcorr 的返回结果就是长度为 2N - 1 的向量。（如果其中一个序列的长度小于 N，则会先补零再计算相关）

用 help xcorr 来查看详细的函数说明。

下面举个使用例子：

1
2
3
4
5
6
7

x = [1, 2, 3];
y = [4, 5, 6];

%correlation
c1 = xcorr(x);
c2 = xcorr(y);
c3 = xcorr(x,y);

对于序列 x = [1, 2, 3]，移位相乘、求和，可以得到结果：

3, 8, 14, 8, 3

对于序列 y 类似。

对于 x、y 的互相关，当两个序列对齐的时候，相关性最高（归一化后为 1，意味着两个序列线性相关）

xcorr 默认的返回结果是没有经过归一化的，而通常的应用中都要求归一化以得到精确的估计。解决这一问题的方法就是使用 xcorr 函数提供的 option 选项：

• 'biased' 有偏估计

• 'unbiased' 无偏估计

• 'coeff' 归一化，返回到最大值（对齐时）为理想的 1.0（= xcorr(x)./max(xcorr(x)) ）

• 'none' 未经归一化的原始数据，默认的返回结果

corrcoef

可以用 corrcoef 函数来求两个序列的相关系数，函数的返回值为一个 2×2 的矩阵，对角线上的值为两个序列的自相关系数，非对角线上的值为两个序列的互相关系数。

在上面的例子中加入下面两句：

1
2

z = [3, 2, 1];
c4 = corrcoef(x,z);

返回结果为

1   -1
-1   1

因为 z 是 x 的线性函数，且系数为 -1，所以非对角线上的值为 -1。

Ref

correlation wiki

pearson wiki

Cross-correlation

Autocorrelation

【总结】matlab 求两个序列的相关性