数字信号处理和相关matlab函数总结
Posted on 2014-09-03 23:16 in Telecom
学了这么多年的通信,却还是对信号处理的知识一知半解,应付考试还可以,但在实际应用中还是感到力不从心,很多知识都忘了。翻了一下午的 《信号与系统》、《数字信号处理》,简单总结一下。
《信号与系统》算是通信专业最基础的专业课了。
信号部分主要介绍信号的相关定义、分类、常用信号和三大变换:傅立叶变换、拉普拉斯变换和 z 变换。
系统部分主要从时域和频域使用不同的方法分析线性时不变系统(LTI)的性质。
《数字信号处理》算是前一门课的深入,现在利用计算机处理信号,首先就是要将模拟信号数字化,然后进行处理。这门课也就是讲相关的知识。
一般教材就讲两大部分:第一部分首先承接《信号与系统》,时域的连续信号要在计算机中处理就必须采样,变为时域离散信号,这部分就讲离散时间信号的处理,比如 z 变换 和离散傅立叶变换。第二部分讲数字滤波器的设计,包括 FIR 和 IIR 两种。
Signal Processing
这部分是我串联的这两本书中很小的一部分知识,算是一个备忘的笔记吧,作为一名学渣,一个月不看也会忘记不少 =.=
从 《信号与系统》 中我们可以知道:
周期信号 (连续)傅立叶级数 (CFS)
首先,由高数知识可以知道:只要满足 Dirichlet 条件,周期信号就可以进行傅立叶级数分解,可以得到幅度频谱和相位频谱。
时域信号是周期的、连续的,频域信号是离散的。
非周期信号 (连续)傅立叶变换 (CFT)
周期信号的周期无限增大,就可以将周期信号转化为非周期信号,从而得到非周期信号的傅立叶变换。
得到的频率域的结果为连续信号,计算结果为时域信号的频谱密度函数,简称频谱函数。
周期信号 (连续)傅立叶变换 (CFT)
对于周期信号,因为它不满足绝对可积的条件,所以从非周期信号无法直接推广。但是借助 奇异函数(如冲激函数)的概念,可以使许多不满足绝对可积的信号(如周期信号)存在傅立叶变换。
周期信号的傅立叶变换结果由一些冲激函数组成,冲激函数的强度是对应的傅立叶级数的 2pi 倍,频谱是离散的。
这样,周期信号和非周期信号的傅立叶分析得到了统一。
接下来,就要进入《数字信号处理》部分了:
离散时间信号傅立叶变换 (DTFT)
时域连续信号经过采样,得到离散时间信号,对于离散时间信号,可以从 z 变换中引出 DTFT 的定义。
DTFT 是一种特殊的傅立叶变换(FT),它满足所有的傅立叶变换的性质。
离散傅立叶变换 (DFT)
虽然 DTFT 解决了信号在时域的连续问题,但是变换结果仍然是连续信号,也就是说在频域仍然是连续的,这样计算机仍然是无法处理的。所以,就引出了离散傅立叶级数(DFS) 和离散傅立叶变换(DFT)。
时域信号的周期性对应着频域的离散化,而且时域信号的离散化对应着频域的周期性。由这两点,可以知道周期的离散信号具有离散的、周期的频谱,也就是离散傅立叶级数(DFS)。
把时域和频域的数据长度都限定在主周期,那么就得到了标准的离散傅立叶变换(DFT)。
经过分析,可以知道,DFT 是 z 变换的取样,也是 DTFT 的取样结果。
DFT 因为是离散的,长度有限,所以很适合计算机计算,而且人们发明了高效地计算 DFT 的方法 —— FFT 。
知乎上还有一篇专栏的文章,得到了非常多人的赞同,可以进一步参考。
Matlab
basic
分析各种变化,可以得到以下的关系:
N 点的 DFT(FFT),其结果对应的
数字角频率 w 为 [0, 2pi)
模拟角频率 Ω 为 [0, Ωs)
模拟频率 f 为 [0, fs)
所以对于 N 点 FFT 的结果,对应的横坐标频率的范围为 [0, fs)。
matlab 提供了函数 fft 和 fftshift 直接完成变换。
adv
我们在对一个信号进行采样分析时,首先需要确定两个参数:参数有采样频率 Fs,采样点数 N,这两个因素决定了之后可以得到的时频域效果。
假设我们的采样频率为 Fs (采样周期为 T = 1/Fs),一共采了 N 个点,那么相当于对信号进行了截断,截断长度为 L = N * T 秒。这 3 个参数就决定了我们的最终结果。
在信号处理中存在下面的 3 个问题:
-
频谱混叠。如果信号不是带限的,那么为了减小频谱混叠的影响,我们应该尽可能提高采样频率 Fs,而且 Fs 越大,时频域分辨率也越高。
-
频率分辨率和栅栏效应。因为 DFT 是 DTFT 的等间隔采样,那么 N 越大,采样点数越多,栅栏就越小。为了提高频率分辨率
f0 = Fs/N,我们应该尽可能增大 N,而且为了提高计算效率,N 等于 2 的 M 次方)。 -
截断效应和频谱泄漏。如果信号是无限长的,那么必须把它截断到长度
L = N*T = N/Fs。截断会带来吉布斯效应,并且引入窗函数的频谱,造成频谱泄漏。应该使得 L 包含信号的绝大部分。
下面举例说明非周期信号和周期信号的分析:
-
非周期信号
假设我们要分析 tau = 1 的矩形窗函数,我们知道它的频谱,且取第一零点 1/tau = 1 为最高频,假设 8 倍采样,即 Fs = 8 Hz,假设频谱分辨率小于 0.1 Hz 即达到需求,则可以得到 N = 128,此时验证 L = 16 满足条件。由 tau 和 Fs 得到采样点包含 8 个 1 和 120 个 0,所以:
1 2 3 4 5 6 7 8
Fs = 8; N = 128; x = [ones(1, 8), zeors(1, 120)]; X = abs(fftshift(fft(x))); f = [0:N-1]*Fs/N - Fs/2; plot(f, X); grid on; xlabel('f / Hz'); ylabel('Amplitude Response'); title('tau = 1 rectangle window');结果如下图:
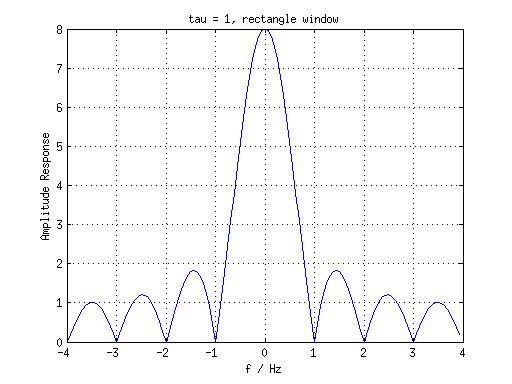
-
周期信号
假设信号为 x = 1 + 1/2cos(2pi15t) + 2sin(2pi40t),包含一个直流分量和 f1 = 15, f2 = 40 Hz 的分量,fm = f2 = 40 Hz,若 8 倍采样,有 Fs = fm*8,若 fdelta < 0.1 hz,有 N = 4096,所以:
1 2 3 4 5 6 7 8 9 10 11 12
f1 = 15; f2 = 40; Fs = f2*8; w1 = 2*pi*f1/Fs; w2 = 2*pi*f2/Fs; n = 0 : N -1; x = 1 + 1/2*cos(w1*n) + 2*sin(w2*n); X = abs(fftshift(fft(x))); f = [0:N-1]*Fs/N - Fs/2; plot(f, X); grid on xlabel('f / Hz'); ylabel('Amplitude Response'); title('x = 1 + 1/2*cos(w1*n) + 2*sin(w2*n)');结果如下:
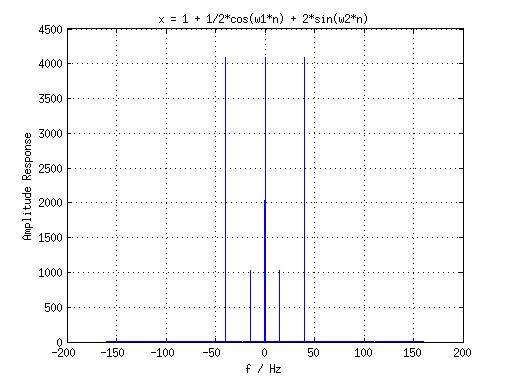
综上,我们就有分析一个信号的通用步骤:
-
首先确定 Fs:信号的频率信息对于我们是未知的,我们最多只知道信号的带宽,根据信号带宽,我们就可以确定一个采样率 Fs,比如 8 倍采样
-
确定了 Fs,实际上的 w 就已经确定了,只是我们是不知道它的具体值(因为不知道 fm)
-
下一步应该确定 N:由公式 1 和公式 2 可以推出
N = Fs/fm*k。当 Fs 最小为奈奎斯特采样速率,k = 1 时,N 取到最小值 2,这种情况下虽然没有混叠,但是 fdelta 太大了,不利于观察频谱,应该由fdelta = Fs/N决定 N 的最小值
====================================== 补充一下 FFT 补零 ========================================
验证程序:假设一个 sin 信号,f = 125, 8 倍采样有 Fs = 1000,
-
N = 8,结果如图:
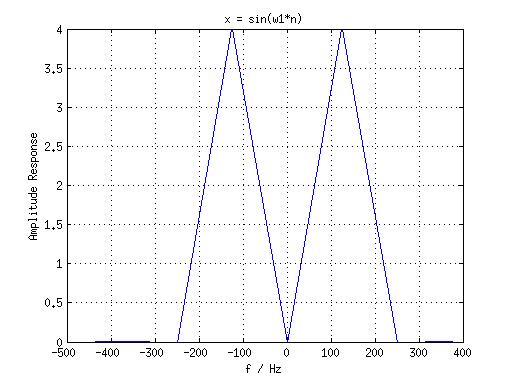
-
N = 8,补零到 64 点,结果如图:
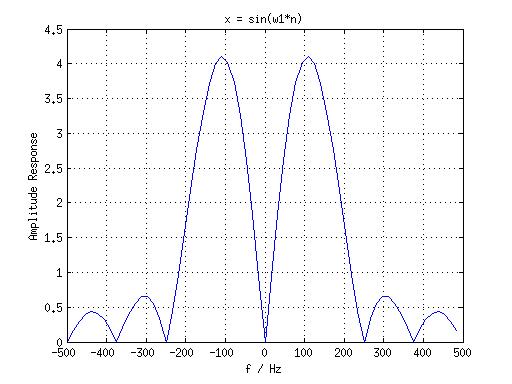
-
N = 64,结果如图:
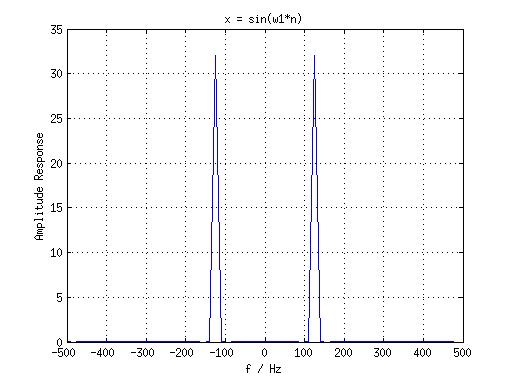
直接给结论(上面的图也证明了这些结论):
-
在时域的采样序列后面添加后缀 0 ,等效在频域内插。频域内插只能从已有的样点推算,因为采样点数不够丢失的原始信号的信息无法通过内插来补偿。
-
时域补零实际上改变了采样序列的,所以频域结果和原始信号不同,
-
补零无法提高频率分辨率,内插出的新分量不是真正物理意义上的频率,是 “ 假频 ”,真正的频率分辨率并没有提高。频率分辨率只能由提高采样点数来提高。