学习 OFDM 及其 FPGA 实现 1 —— OFDM Basic
Posted on 2014-05-13 23:16 in Telecom
Why OFDM
Background
移动通信的信道模型一般建立为 时变多径信道模型,描述信道多径时延特性的一个重要统计参量是 均方根时延扩展 。
经过无线信道的时变多径传输,接收到的信号幅度会有起伏变化(瑞利分布 or 莱斯分布),这种现象称为 信号衰落 。按照已调信号的带宽可以将衰落分为两类:
- 窄带信号受到 平坦性衰落
- 宽带信号受到 频率选择性衰落 。
判断信号受到何种衰落:
定义信道的 相干带宽 。当数字信号的带宽越小于信道的相干带宽,则经过时变多经信道后,在信号带宽内的不同频率分量的幅度的相关性越大,不同的频率分量近似经历相同的衰落,即平坦性衰落,平坦性衰落对接收信号的波形无明显影响,码间干扰可以忽略,该系统称为 窄带系统 。当数字信号的带宽相对于信道的相干带宽越大时,信号带宽内的不同频率分量通过信道传输时会受到不同的衰落,即频率选择性衰落,频率选择性衰落使信号中的不同频率分量产生不同的幅度变化,造成接收信号的严重失真,引起吗见干扰,产生误码,该系统称为 宽带系统 。
Problem
需求
无线信道的频率资源是有限的,要求数字通信系统有效利用信道频带。希望数据传输速率越高越好。
瓶颈
在系统设计选择数字调制方式时,必须兼顾 频带利用率 和 误码性能 。在 AWGN 信道下,在满足误码性能的前提下,应该尽可能采用频带利用率高的数字调制方式。
然而,在以衰落为特征的移动通信系统中,影响误码性能的不仅仅是 加性噪声,还包括 衰落 和 码间干扰 。实现高速无线通信并非易事。
为避免码间干扰,数字调制信号的最大符号速率受到很大的限制 。
Solution
信道均衡 是一种经典的对抗码间干扰的技术,许多移动通信系统都采用信道均衡技术消除码间干扰。但是如果数据速率非常高,采用单载波传输数据,需要设计几十审计上百个抽头的均衡器,这简直是硬件设计的噩梦 。
既要对抗码间干扰,又要满足低复杂度且高效的手段传输高速数据业务,我们可以采用另外一种技术 —— OFDM 。
OFDM History
多载波调制技术早在 20 世纪 50 年代末至 60 年代初就已经应用于军事高频无线通信中,由于实现复杂,没有被广泛应用 。OFDM 就是一种多载波调制,其子载波间隔是子载波符号间隔的倒数,各子载波的频谱是重叠的,这种重叠可以使频谱效率显著提高 。
20 世纪 70 年代,Weinstein 和 Ebert 提出用 离傅里叶变换 (DFT) 及其 逆变换 (IDFT) 进行 OFDM 多载波调制方式的运算。
DFT 和 IDFT 的快速计算方法:FFT 和 IFFT 使 OFDM 能够以低成本的数字方式实现 。
在 20 世纪 80 年代,随着 OFDM 理论的不断完善、数字信号处理及微电子技术的不断快速发展,OFDM 技术也逐步走向实用化 。
大约从 20 世纪 90 年代起,OFDM 技术开始应用于各种有线及无线通信中,包括:DSL、DAB、DVB、WLAN 等。OFDM 已经成为下一代蜂窝移动通信空中接口的候选技术 。
OFDM Theory
Orthogonal frequency-division multiplexing (OFDM) 的基本原理是将高速的数据流分解为多路并行的低速数据流,在多个载波上同时进行传输。
通过将高速数据分解为多个并行低速速率,克服了信道时延扩展对数据速率的限制,其中各个子载波之间是相互正交的关系,如图:

OFDM 每个子载波的调制方式可以相互不同,比如 BPSK、QPSK、QAM 等方式 。
(OFDM 系统的内容可以写一本书了,简单写写 :-P )
OFDM 基带数字实现
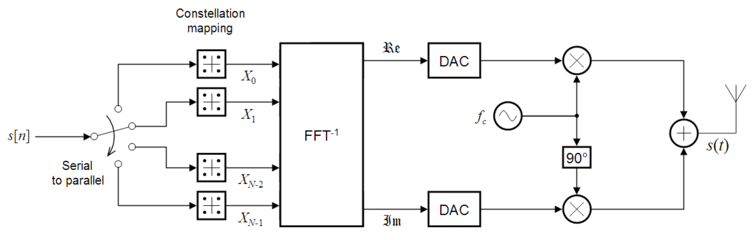
发送端 Transmitter
基带系统发送端要实现的功能是将待发送序列 {A1,A2,A3...} 变换,得到复包络的采样值 {a1,a2,a3...} 。
为了实现 OFDM 调制的基带数字实现,首先要将 OFDM 信号的复包络进行采样,成为离散时间信号 。根据公式 (《通信原理》),采样结果正好是对发送序列进行离散傅里叶反变换 (IDFT) 的结果,所以,我们可以 借助 IDFT 即可得到 OFDM 复包络的时间采样 。
发送端框图:
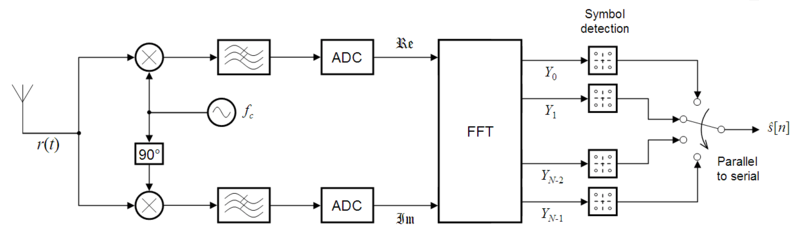
接收端 Receiver
基带系统接收端要实现的功能是对采样序列 {a1,a2,a3...} 进行变换,得到发送端发送过来的信息序列 {A1,A2,A3...} 。
接收端通过 I/Q 正交解调可以恢复 OFDM 信号的复包络,将其采样得到的时间序列 。因为发送端采用的 IDFT 是可逆变换,所以对采样结果进行 DFT 就可以得到发送序列 。
当序列的点数为 2 的整幂次时,DFT 和 IDFT 存在快速算法: FFT 和 IFFT 。
接收端框图:
循环前缀 cyclic prefix
为了有效对抗多径信道的时延扩展,OFDM 系统由多个子载波构成,只要子载波的取值可以满足符号周期远大于信道的时延扩展,就可以达到目标。在此基础上,还需要采取措施消除前后两个 OFDM 符号之间的 码间干扰 ISI 。
一种方法是在每个 OFDM 符号之间插入 保护间隔 Guard Interval 。为了对抗信号因信道延迟的影响,Gurad interval(Tg) 长度要大于最大的 Delay spread,即 Tg > delay spread time。
在保护区间未放信号的 OFDM 系统称 ZP-OFDM(zero padding)。ZP-OFDM 有比较低的传输功率,但在接收端接收于 zero padding 区域信号时,会破坏载波的正交性造成 “载波间的干扰(ICI)”,所以复制 OFDM symbol 后半段信号并摆放于保护区间内,称之为 循环字首 (cyclic prefix) 。
加窗技术
前面介绍了 OFDM 符号的生成、循环前缀消除码间干扰,但是此时符号边界有尖锐的相位跳变,由此可知,OFDM 的带外衰减是比较慢的 。虽然随着载波数目的增大,OFDM 信号的带外衰减会增加,但是仍然不够快 。
为了使 OFDM 信号的带外衰减更快,可以采用对单个 OFDM 符号加窗的方法 。OFDM 的窗函数可以使信号的幅度在 u 符号边界更平滑地过渡到 0 。常用的窗函数是 升余弦滚降窗 。
增大滚降因子虽然能够使带外衰减更快,但降低了 OFDM 系统对多经实验的容忍能力,所以 在实际系统设计中,应当选择较小的滚降因子 。
OFDM 系统设计
OFDM 系统框图如下:
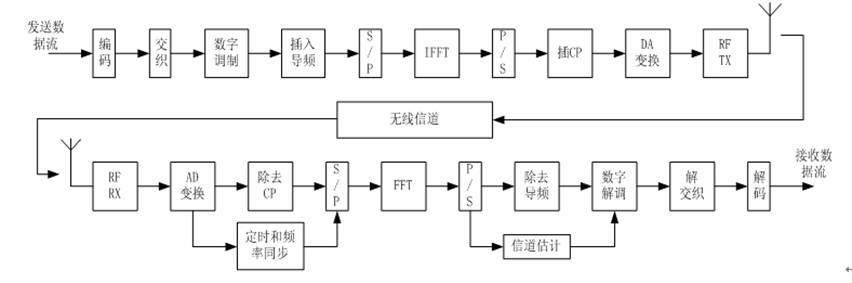
其中,交织 是为了克服深衰落发生突发差错的影响,如果交织器的长度足够大,解交织后可将突发差错改造为独立差错,再通过纠错译码来纠正 。
在发送端:
二进制数据 通过纠错编码、交织后映射到 QAM 星座得到 一个 QAM 复数符号序列,再经过并串转换,得到 N 个并行 QAM 符号,每个符号进行 IFFT,将 OFDM 复包络的频域样值变换为 时域样值,进行并串转换,将时域样值变换为按时间顺序排列的 时域样值,然后在每个 OFDM 符号前插入前缀,通过 D/A,将离散的复包络变成 连续时间的复包络 。再将复包络的 I(t) 和 Q(t) 正交调制得到 OFDM 信号,将基带信号上变频到射频,经过功放,发送出去 。
在接收端:
接收端于发送端进行相反的变换,恢复出原数据 .